Для критических давлений мы сохранили вид зависимости, использованный для критических температур и обладающий достаточной гибкостью. В отличие от критических температур при определении вида корреляции (5.13) использованы экспериментальные данные не только для н-алканов, но также для н-спиртов и н-карбоновых кислот. Дополнение класса алканов спиртами и кислотами обусловлено необходимостью расширения корреляции в область высоких давлений, которая не перекрывается алканами. Следует подчеркнуть, что критические давления не потребовали специальных корреляций для ассоциированных жидкостей. Это оказалось возможным потому, что при прогнозировании не использовалось какое-либо опорное свойство вещества, особенно такое, которое не передает специфику его поведения в критическом состоянии.

Обращаем внимание на некоторые особенности прогнозирования критических давлений веществ, склонных к сильным специфическим взаимодействиям. Дело в том, что присутствие в молекуле групп типа -ОН, -СООН, - NH ₂ и т.п. приводит к существенно более высокому критическому давлению по сравнению с гомоморфами веществ, не содержащими таких групп. Подобное соотношение в свойствах требует использования отрицательных значений кодовых чисел для указанных групп. Однако алгоритм Рандича не допускает применения отрицательных величин d _i . Мы сочли целесообразным внесение некоторых корректив в метод (для подобных веществ) при сохранении алгоритма Рандича. Коррективы состоят в следующем. Все члены уравнений для расчета индексов молекулярной связности, содержащие кодовые числа групп, склонных к специфическим взаимодействиям, участвуют в расчете со знаком “минус”. Процедура расчета и некоторые особенности прогнозирования Р_с изложены ниже на примере соединений некоторых классов.

Алканы

Для алканов расчет поправки производится в едином алгоритме Рандича для всех цепочек последовательно соединенных атомов, каждая из которых включает два и более третичных и (или) четвертичных атомов углерода, по формуле

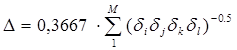, (5.14)

что эквивалентно 0,3667× для взаимодействующих групп.

Результаты прогноза критических давлений (табл. 5.7) показывают, что для выборки из 68 соединений среднее абсолютное отклонение в оценках составляет 0,29 бар, относительное отклонение – 1,30% отн., что в три раза меньше, чем в методах Лидерсена или Джобака. При одинаковом количестве парциальных вкладов (по одному значению для первичного, вторичного, третичного и четвертичного атомов углерода) методы обладают существенно различающимися прогностическими возможностями. Отчасти это обусловлено менее жестким видом корреляции (5.13) по сравнению с (5.11) и (5.12), отчасти - дополнительными алгоритмическими возможностями метода, основанного на индексах молекулярной связности.

Максимальная погрешность метода равна 3,8% отн. для н-тридекана. Для трех соединений (н-тридекан, н-тетрадекан и 3,3-диэтилпентан) погрешность выше 3% отн., и для 16 алканов, 10 из которых - линейные алканы, погрешность выше 2 % отн.

Алкены

На основе экспериментальных данных для 46 алкенов определены с достаточно высоким статистическим весом значения 3 кодовых чисел (табл. 5.8) для ненасыщенных углеродных атомов с различной степенью замещения. Аналогично критическим температурам критические давления алкенилбензолов не требуют самостоятельных кодовых чисел для ненасыщенных  -углеродных атомов. Результаты прогнозирования Р_с алкенов с использованием полученных кодовых чисел и уравнения (5.13) приведены в табл. 5.7 и являются вполне удовлетворительными. Среднее абсолютное отклонение в оценках составляет 0,62 бар (2,15 % отн.). Методы Лидерсена и Джобака дают близкие результаты.

Необходимо отметить, что нам не известны сведения по Р_с алкенов, имеющих два и большее количество разветвленных заместителей при двойной связи. Не исключено, что по мере расширения базы данных потребуются некоторые коррективы в методе. Эти коррективы, вероятнее всего, будут касаться преимущественно подхода к оценке поправок (). Для веществ без значительных разветвлений при двойной связи, которые рассмотрены нами, не потребовалось вводить какие-либо специфичные для алкенов поправки сверх тех, которые касаются насыщенной части молекул и представлены уравнением (5.14) (все атомы в цепочках при вычислении поправок являются насыщенными).

Алкилбензолы, метилнафталины и метилпиридины

Аналогично критическим температурам для критических давлений соединений указанных классов потребовалось дополнение схемы четырьмя кодовыми числами:

· для незамещенного атома углерода ароматического ядра;

· для замещенного атома углерода ароматического ядра;

· для узловых атомов в нафталинах:

· для атома азота в пиридинах.

Все величины определены со значительным статистическим весом (табл. 5.8).

Так же как и для критических температур, при прогнозировании критических давлений особенности поведения орто-замещенных структур хорошо передаются алгоритмически и не требуют введения в расчетную схему дополнительных кодовых чисел сверх указанных в табл. 5.8. Поправки на орто-взаимодействие между собой алкильных заместителей в алкилбензолах и пиридинах, а также взаимодействия алкильного заместителя с вторым ароматическим ядром в -замещенных нафталинах вводятся при расчете дополнением уравнения (5.13) поправкой, вычисляемой по уравнению (5.15):

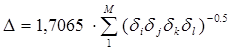(5.15)

с кодовыми числами для Р_с (табл. 5.8). При этом необходимо иметь в виду, что уравнение (5.15) получено на экспериментальной базе, ограниченной метил- и этилпроизводными ароматическими углеводородами, т.е. не исключено, что увеличение эффективных размеров алкильных заместителей потребует внесения корректив в метод.

Так же, как и для критических температур, в данном случае не потребовалось дополнительной детализации метода для  -углеродных атомов алкильных заместителей, т.е. увеличение размеров и степени разветвления заместителей не должно изменить уровня погрешностей при прогнозировании Р_с соединений с изолированными заместителями.

При использовании уравнения (5.13) и кодовых чисел (табл. 5.8) метод дает среднее отклонение для алкилбензолов, метилнафталинов и полифенилов 0,59 бар (2,14% отн.). Методы Лидерсена и Джобака для той же выборки дают отклонения 1,10 бар (3,49% отн.) и 1,09 бар (4,12% отн.) соответственно.

Обращает на себя внимание тот факт, что все методы дают существенно более низкие (на 3.5-5.8 бар) оценки критических давлений для 1,2- и 1,4-дифенилбензолов.

Класс алкилпиридинов представлен только моно- и диметилзамещенными соединениями, хинолин и изохинолин не имеют заместителей. Анализ имеющихся экспериментальных данных показал, что для метилпиридинов (МП), в том числе и для 2,6-диМП, не требуется вводить какие-либо поправки, учитывающие взаимодействие заместителя с соседним атомом азота в ароматическом ядре. Для соединений с соседними метильными группами, например 3,4-диМП, поправка вводится обычным порядком по уравнению (5.15).

Для выборки из 12 соединений среднее абсолютное отклонение составляет 0,89 бар (2.00% отн.), 3,15 бар (7,00% отн.) и 1,15 бар (2,61% отн.) для методов с индексами Рандича, Лидерсена и Джобака соответственно. Метод Лидерсена дает заниженные оценки для большинства пиридинов.

Сведения по критическим давлениям алкилфенолов (АФ) ограничены моно- и диметилпроизводными, моноэтилфенолами и 4-третбутилпирокатехином. Для указанных веществ при прогнозировании достаточно дополнить набор кодовых чисел (табл. 5.8) одним значением - для “ОН” группы. Не исключено, что стерически напряженные структуры потребуют расширения набора параметров. Для неэкранированных фенолов, вероятнее всего, таких дополнений не потребуется.

Как было отмечено выше, при расчете фенолов все слагаемые уравнения вводятся со знаком “минус”. Например, для 2,6-диметилфенола имеем:

=-1/(1,0456·4,391)^0,5 +2/(1·4,391)^0,5 +2/(4,391·4,391)^0,5 +

+2/(4,391·5,693)^0,5 +2/(5,693·5,693)^0,5 -2/(1,0456·4,391·4,391)^0,5 +

Значение поправки вычисляется по уравнению (5.15). Для 2,6-диметил-фенола имеем

D=1,7065 [2/(1·4,391·4,391·1,0456)^0,5 +1/(1·4,391·4,391·4,391·1)^0,5 ]=0,5541.