сложение матриц, имеющих один и тот же размер;

умножение матриц подходящего размера (количество строк одной матрицы должно совпадать с количеством столбцов другой); умножение матрицы на элемент основного кольца или поля (т. н. скаляр).

Относительно сложения матрицы образуют абелеву группу; если же рассматривать ещё и умножение на скаляр, то матрицы образуют векторное поле над соответствующим кольцом или полем. Для квадратных матриц матричное умножение является замкнутой операцией, поэтому квадратные матрицы одного размера образуют кольцо относительно матричного сложения и матричного умножения.

В математике рассматривается множество различных типов и видов матриц.

Особое значение в теории матриц занимают всевозможные нормальные формы. Наиболее важной (в теоретическом значении) и проработанной является теория жордановых нормальных форм. На практике, однако, используются такие нормальные формы, которые обладают, например, устойчивостью.

Схема алгоритма программы

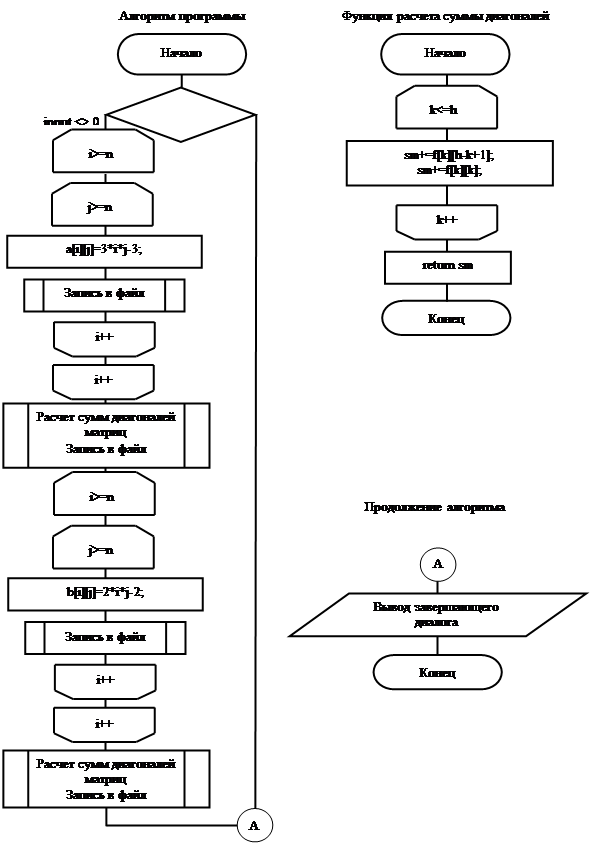Разработка си-программы

Для реализации алгоритма и решения задачи, а в частности генерирования значений элементов матрицы, нахождения суммы, запись результата в файл необходима реализация цикла FOR.

Необходимые константы:

const int n=10; для определения размера матриц;

переменные:

i,j,sтипа int;

массивы:

a [n] [n],b [n] [n] типа int;

файловые указатели:

char* fname="c: \\data.txt";

FILE*input;

Функция для расчета суммы диагоналей матриц intsumm (intf [n] [n], int).

Вывод данных реализовываем с помощью форматного ввода-вывода языка С.

Исходный текст си-программы

#include<stdio.h>

#include <conio.h>

#include <math.h>

const int n=10; // Постоянная переменная размерности массива

int a [n] [n],b [n] [n], i,j,s; // массивы

intsumm (intf [n] [n], int); // прототип функции вычисления суммы диагоналей

char* fname="c: \\data.txt"; // файловый указатель

FILE*input; // указатель файловой переменной

voidmain ()

{input=fopen (fname,"w"); // открываем файл для записи

if (input! =0) { // проверка отрылся ли файл