БЕЛОРУССКИЙ НАЦИОНАЛЬНЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Международный институт дистанционного образования

Кафедра "Информационные системы и технологии"

Реферат

по учебной дисциплине

"Языки программирования"

ТЕМА РАБОТЫ:

"Программирование математических задач"

Руководитель: Кондратенок Е.В.

Исполнитель: студент 417319/14

учебной группы Кодатенко Ю.А.

Минск 2010

Содержание

Введение

Введение

Постановка задачи

Постановка задачи

Теоретические основы

Схема алгоритма программы

Разработка си-программы

Результаты выполнения

Заключение

Литература

Введение

Си - стандартизированный процедурный язык программирования, разработанный в начале 1970-х годов сотрудниками Bell Labs Кеном Томпсоном и Денисом Ритчи как развитие языка Би. Си был создан для использования в операционной системе UNIX. С тех пор он был портирован на многие другие операционные системы и стал одним из самых используемых языков программирования. Си ценят за его эффективность. Он является самым популярным языком для создания системного программного обеспечения. Его также часто используют для создания прикладных программ. Несмотря на то, что Си не разрабатывался для новичков, он активно используется для обучения программированию. В дальнейшем синтаксис языка Си стал основой для многих других языков.

Постановка задачи

Составить алгоритм и программу на языке Си для формирования двух матриц A= [ aij] и B= [ bij] размерностью nxn ( n=10), значения элементов aij иbij определяются по формулам (1). Определить сумму элементов, расположенных на диагоналях каждой матрицы.

Исходные данные:

(1)

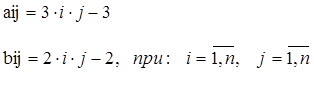
Для вычисления сумм использовать функцию.

Матрицы Aи Bи результаты вычисление сумм вывести в файл.

Теоретические основы

Матрица - математический объект, записываемый в виде прямоугольной таблицы элементов кольца или поля, которая представляет собой совокупность строк и столбцов, на пересечении которых находятся её элементы. Количество строк и столбцов матрицы задают размер матрицы.

Матрицы широко применяются в математике для компактной записи систем линейных алгебраических или дифференциальных уравнений. В этом случае, количество строк матрицы соответствует числу уравнений, а количество столбцов - количеству неизвестных. В результате, решение систем линейных уравнений сводится к операциям над матрицами.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--