Після інтегрування одержуємо

(3.2.1.4)

Формула (3.2.1.4) показує, що чим більша стала розпаду l, тим швидше розпадаються радіоактивні ядра. Порівнюючи (3.2.1.3) і (3.2.1.4) , бачимо, що Т і мають один і той же порядок, причому

3.2.2 Закономірності альфа - і бета – розпаду

а). Механізм альфа – розпаду

Явище альфа – радіоактивності було відкрите при вивченні радіоактивності природних елементів. Природні a - випромінювачі розміщуються в таблиці Менделєєва, починаючи з номера Z³ 82 (Z=82 має свинець). Оскільки в a - частинці питома енергія зв’язку виявляється більшою, ніж у важких ядрах, a - розпад енергетично є завжди можливим. Наприклад, нуклід урану ²³⁸ U випромінює a - частинки з періодом піврозпаду 4,5·10⁹ років.

Самочинно відбувається ядерна реакція

МеВ. (3.2.2.1)

Різниця мас і продуктів розпаду складає 4,2 МеВ. (Маса материнського ядра перевищує суму мас продуктів розпаду на DМ = 0.0045 а.о.м.).

Правило зміщення для a- розпаду записують так:

, (3.2.2.2)

де - материнське ядро; - дочірнє ядро; частинка; g-гамма - квант, який звільняється дочірнім ядром при переході у менш збуджений або нормальний стан.

Процес a- розпаду має дві особливості, які були відкриті експериментально.

Між пробігом a-частинки, який може бути мірою її початкової енергії і сталою радіоактивного розпаду l є проста залежність, емпірично встановлена Гейгером і Неттолом ще у 1911 році і відома під назвою закону Гейгера-Неттола:

(3.2.2.3)

де А і В – сталі величини, причому стала В є однаковою для всіх радіоактивних елементів; А – є сталою лише в межах певного радіоактивного ряду.

Із закону Гейгера – Неттола випливає, що чим менш стабільні ядра, тим більша енергія у a-частинок, які при цьому випромінюються.

Наступною особливістю a- розпаду є досить низька енергія a- частинок у момент вилітання із ядра, яка змінюється в межах 4–9 МеВ. Насправді a- частинки у момент вилітання із ядра повинні мати значно більшу енергію, рівну висоті потенціального бар’єра. В реакції 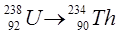потенціальна енергія відштовхування a- частинки на межі ядра торію складає біля 30 МеВ . Відповідно a- частинка після подолання такого бар’єра повинна прискоритися до 30 МеВ . Експериментально ж виявлені a- частинки з енергією 4.2 МеВ .

Чому енергія a- частинок порівняно невисока, та як можна пояснити закон Гейгера-Неттола? Відповідь на ці запитання дає квантова механіка.

Перед початком a- розпаду в багатьох ядрах уже існує по одній a-частинці. Енергія такої частинки . Якби не було потенціального бар’єра, a- частинка вилітала б із ядра з енергією (рис. 3.2.1).

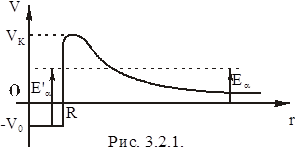
На рис. 3.2.1 V₀ – глибина потенціальної ями; - енергія a- частинок після вилітання із ядра.

Таке враження, що, залишаючи ядра, a- частинки не помічають існування потенціального бар’єра.

Згідно з законами квантової механіки a- частинки проявляють хвильові властивості. При попаданні на стінку потенціального бар’єра вони відбиваються від неї як хвилі. Але не всі a- частинки відбиваються від стінки. Частина із них проникає крізь стінку і залишає ядро з енергією Е_a . Ефект проникнення a- частинок крізь потенціальний бар’єр при енергіях значно нижчих його висоти називається тунельним ефектом .

Імовірність проникнення a- частинок крізь потенціальний бар’єр визначається його прозорістю Д . При цьому стала радіоактивного розпаду l, яка визначає імовірність розпаду за одиницю часу, дорівнює добутку “ прозорості “ бар’єра на число зіткнень n a- частинки з внутрішніми стінками бар’єра, тобто

l = Д n , (3.2.2.3)

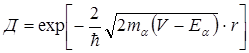, (3.2.2.4)

де m _a - маса частинки, r – ширина потенціального бар’єра; n – число ударів a- частинки об стінку потенціального бар’єра; Д – прозорість бар’єра у цьому місці.

Мала прозорість Д бар’єра для проникнення крізь нього a- частинки пояснює малу імовірність a- перетворення (мала стала розпаду l) і великий період піврозпаду. Це і є пояснення закону Гейгера – Неттола.