Реферат: Радиолокационная станция обнаружения воздушных целей

Определим значение максимальной дальности обнаружения D_max которую должна иметь РЛС в свободном пространстве, чтобы ее дальность действия при наличии поглощения радиоволн в атмосфере была равна заданному значению D_{max п} .

, (1.22)

где a(l) - коэффициент потерь энергии радиоволн в атмосфере, определяемый по графику в [ ]

дБ/км.

Тогда

км.

Находим произведение средней мощности передатчика на эффективную площадь антенны:

, (1.23)

где - эффективная отражающая площадь поверхности цели.

Вт*м² .

Найдем значение средней мощности передатчика:

Вт. (1.24)

Найдем стоимость РЛС:

. (1.25)

Определим значение средней мощности передатчика и эффективную площадь антенны по критерию минимума стоимости РЛС на первой итерации:

Вт, (1.26)

м² . (1.27)

Определим теперь значение длины волны, соответствующее рассчитанным величинам. Так как в нашей РЛС используется совмещенная антенна, то и связаны соотношением:

. (1.28)

и следовательно:

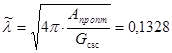м. (1.29)

Проверим выполнение условия:

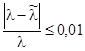, (1.30)

. (1.31)

где .

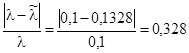
Так как ни одно из условий не выполняется, проведем оптимизацию параметров на ЭВМ. Значение стоимости РЛС и длины волны на каждой итерации сведены в табл. 1.1.

Результаты расчетов до оптимизации и параметров РЛС после проведения оптимизации на ЭВМ приведены в приложении 1.

Таблица 1.1

№ итерации	Длина волны на предыдущей итерации	Стоимость РЛС на предыдущей итерации	Новая граница длины волны
1	0,1 м	67564	0,134 м
2	0,134 м	52252	0,12 м
3	0,12 м	44958	0,125 м
4	0,125 м	43489	0,124 м
5	0,124 м	42252	Оптимально

Под стоимостью С₁ понимают взвешенную сумму 1 Вт мощности передатчика и 1 м² антенны. В результате оптимизации стоимость РЛС уменьшилась с 67564 до 42252, была получена оптимальная длина волны l = 0,124 м, которая больше длины волны до оптимизации (l = 0,1 м). Это приводит к тому, что при фиксированном коэффициенте усиления антенны произошло увеличение ее эффективной площади. Энергетический потенциал станции фиксирован, следовательно при увеличении эффективной площади антенны происходит уменьшение средней мощности передатчика.

2. ВЫБОР И РАСЧЕТ ПАРАМЕТРОВ ЗОНДИРУЮЩИГО СИГНАЛА

После оптимизации мы получили базу сигнала равную В = 8. Из-за того, что база сигнала больше единицы возникает противоречие между максимальной дальностью и разрешающей способности по дальности. При использовании простого сигнала это противоречие невозможно обойти, однако использование сложных сигналов позволяет обеспечить требуемые параметры. Наиболее известными сложными сигналами являются фазоманипулированные сигналы (ФМ) и сигналы с линейной частотной модуляцией (ЛЧМ). Из курса лекций М.Б.Свердлика и А.Н.Мелешкевича известно, что при базе сигнала меньше 20 предпочтительней использовать ФМ сигнал.

Аналитическое описание фазоманипулированного сигнала имеет вид:

, (2.1)

где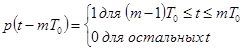

Свойство фазоманипулированных сигналов при заданных М и Т₀ полностью описываются кодовой последовательностью:

(2.2)

Среди фазоманипулированных сигналов наибольшее распространение получили бифазные сигналы , которые строятся на базе кодовых последовательностей максимальной длины (КМД) или М-последовательностей . Между значениями Y_m и значениями X_m М-последовательности, имеется однозначное соответствие:

Рассмотрим ФМ сигнал для нашей РЛС.

ГГц

мкс

М-последовательность является переодической с периодом , который должен быть не меньше базы сигнала. Таким образом В = 7.51 @ 8, и следовательно, М ³ 8. При m = 4 получим М = 15, где m – степень порождающего полинома М-последовательности.

Сгенерируем М-последовательность с минимальным уровнем боковых лепестков функции автокорреляции. Величина боковых лепестков зависит от вида порождающего полинома и от начальной комбинации. Воспользуемся таблицами, приведенными в методических указаниях [4].

(2.3)

Согласно этому полиному (2.3) и для начальной комбинации 1000, построим структурную схему генератора ФМ сигнала:

Рис.2.1 Структурная схема генератора ФМ сигнала

Построим М-последовательность, реализованную схемой изображенной на рис.2.1. Результаты сведем в табл.2.1.

Таблица 2.1

Х4	0	0	0	1	1	1	1	0	1	0	1	1	0	0	1
Х3	0	0	1	1	1	1	0	1	0	1	1	0	0	1	0
Х2	0	1	1	1	1	0	1	0	1	1	0	0	1	0	0
Х1	1	1	1	1	0	1	0	1	1	0	0	1	0	0	0
Х0	1	1	1	0	1	0	1	1	0	0	1	0	0	0	1

0	0	0	1	1	1	1	0	1	0	1	1	0	0	1
1	0	0	0	1	1	1	1	0	1	0	1	1	0	0	1
0	1	1	1	0	0	0	0	1	0	1	0	0	1	1
0	1	1	1	0	0	0	0	1	0	1	0	0	1
1	0	0	0	1	1	1	1	0	1	0	1	1
1	0	0	0	1	1	1	1	0	1	0	1
0	1	1	1	0	0	0	0	1	0	1
1	0	0	0	1	1	1	1	0	1
0	1	1	1	0	0	0	0	1
1	0	0	0	1	1	1	1
1	0	0	0	1	1	1
1	0	0	0	1	1
1	0	0	0	1
0	1	1	1
0	1	1
0	1
1	0	1	2	1	2	1	0	1	0	3	2	1	0	15

Рис. 2.2 Построение огибающей ФМ сигнала на выходе согласованного фильтра

Схема, изображенная на рис.2.1 работает следующим образом. Генератор тактовых импульсов ГТИ вырабатывает тактовые импульсы с периодом Т₀ . Делитель частоты делит частоту тактового импульса до частоты повторения зондирующего сигнала. Формирователь управляющих импульсов длительностью МТ₀ (ФУИ МТ₀ ) синхронизируется сигналами с выхода делителя частоты (а также с блока синхронизации нестабильности линии задержки ЧПК) и формирует импульсы длительностью МТ₀ . Эти импульсы включают коммутатор, подключенный к генератору гармонического колебания. В зависимости от кода М-последовательности (0 или 1) на выходе коммутатора получаем гармоническое колебание со сдвигом фазы 0 или p соответственно.

Рассмотрим автокорреляционную функцию полученного сигнала, которая будет соответствовать комплексной огибающей на выходе согласованного фильтра.