Реферат: Расчет элементов высокочастотной коррекции усилительных каскадов на биполярных транзисторах

;

;

(5.4)

– входное сопротивление и входная емкость каскада.

Значение , соответствующее оптимальной по Брауде АЧХ, рассчитывается по формуле:

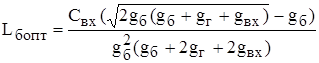. (5.5)

При заданном значении и расчете по (5.5) верхняя частота полосы пропускания входной цепи равна:

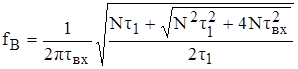, (5.6)

где .

Пример 5.2. Рассчитать , , входной цепи, приведенной на рис. 5.2, при использовании транзистора КТ610А (данные транзистора приведены в примере 2.1) и условий: = 50 Ом, = 0,9, допустимое уменьшение за счет введения корректирующей цепи – 5 раз.

Решение. Из примера 5.1 имеем: = 126 Ом, = 196 пФ, = 0,716. Используя соотношение (5.3) и условия задачи получим: = 10 Ом. Подставляя в (5.5) найдем: = 7,54 нГн. Подставляя результаты расчетов в (5.6), получим: = 108 МГц. Используя соотношения (5.4), (2.5) определим, что при простом шунтировании каскада резистором = 10 Ом каскада оказывается равной 50 МГц.

5.3. РАСЧЕТ КАСКАДА С ПАРАЛЛЕЛЬНОЙ ОТРИЦАТЕЛЬНОЙ ОБРАТНОЙ СВЯЗЬЮ

Для исключения потерь в усилении, обусловленных использованием входной корректирующей цепи (см. раздел 5.2), в качестве входного каскада может быть использован каскад с параллельной ООС. Принципиальная схема каскада приведена на рис. 5.3,а, эквивалентная схема по переменному току - на рис. 5.3,б.

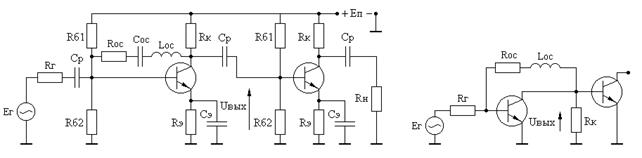
а) б)

Рис. 5.3

Особенностью схемы является то, что при большом значении входной емкости нагружающего каскада и глубокой ООС ( мало) в схеме, даже при условии = 0, появляется выброс на АЧХ в области верхних частот. Поэтому расчет каскада следует начинать при условии:= 0. В этом случае коэффициент передачи каскада в области верхних частот описывается выражением:

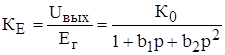, (5.7)

где ; (5.8)

;

;

;

– входное сопротивление и емкость нагружающего каскада.

При заданном значении , каскада равна:

, (5.9)

где .

Формулой (5.9) можно пользоваться в случае, если . В случае схема имеет выброс на АЧХ и следует увеличить . Если окажется, что при меньше требуемого значения, следует ввести . В этом случае коэффициент усиления каскада в области верхних частот описывается выражением:

, (5.10)

где ; (5.11)

;

;

;

.

Оптимальная по Брауде АЧХ достигается при условии:

. (5.12)

При заданном значении , каскада может быть найдена после нахождения действительного корня уравнения:

, (5.13)