Реферат: Расчет конусной дробилки крупного дробления ККД 500 75

Рис. 4.3 Разгрузка дробленого продукта из конусной дробилки

крупного дробления при наивыгоднейшей частоте вращения

эксцентрикового стакана

Высоту h находим из геометрических соотношений. Проводим из точки К, которую займет точка N поверхности дробящего конуса, когда он придет в крайнее правое положение, линию KN₁ параллельную AA₁ , и проводим плоскость A₁ N₁ , с горизонта которой куски дробленого продукта должны еще выпасть из дробилки при отходе конуса. Из треугольника NN₁ K получим

где γ₁ и γ₂ - углы между образующими поверхностей дробящего конуса и на­ружной чаши с вертикалью.

Пользуясь свойством производной пропорции можно написать

где S - ход дробящего конуса на горизонте разгрузочного отверстия, равный двойному эксцентриситету , м.

Конусные дробилки крупного дробления работают с числом оборотов, которое приблизительно в 2 раза меньше, чем по теоретической формуле (4.1). Отклонение можно объяснить тем, что при выводе формулы не учтены различ­ные сопротивления, которые встречает материал при выходе из дробилки. Для практических расчетов частоты вращения эксцентрикового стакана пользуются формулой

Промышленные испытания показывают, что с увеличением частоты вра­щения эксцентрика (в некоторых пределах) производительность дробилки рас­тет, по-видимому, сказывается повышение скорости прохождения материала при повышении частоты колебаний конуса. Поэтому при проектировании дро­билок частоту вращения эксцентрика назначают из условий обеспечения на­дежной работы подшипникового узла эксцентрикового стакана, а также учиты­вают уравновешенность дробилки на фундаменте.

В современных конусных дробилках крупного дробления эксцентриситет на уровне разгрузочной щели составляет 13-25 мм в зависимости от размера дробилки. Дробилки одного размера могут иметь разные эксцентриситеты. Анализ конструктивных размеров дробилок показывает, что средний ход кону­са на горизонте выходной щели (двойной эксцентриситет) связан с шириной приемного отверстия В прямолинейной зависимостью S = 0,02В + 0,01, где В и S приняты в метрах.

Подставив в формулу (4.1) найденное значение S и численные значения тангенсов углов наружной чаши и дробящего конуса получим

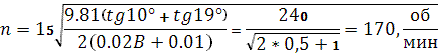
Производительность

Определим объем V дробленого продукта, выпадающего из дробилки за один оборот эксцентрикового стакана, работающей с наивыгоднейшей частотой вращения (см. рис. 4.3). Куски, расположенные выше плоскости A ₁ N₁ , не вый­дут из рабочего пространства дробилки, так как их размер больше максималь­ной ширины выходной щели. За один оборот эксцентрикового стакана из дро­билки выпадает дробленый продукт, занимающий объем кольца с трапецеи­дальным поперечным сечением AA₁ N₁ N. Это кольцо представляет собой про­странство, получающееся при вращении трапеции AA₁ N₁ N вокруг оси корпуса дробилки OO₁ . Согласно теореме Гульдена объем такого пространства равен произведению площади фигуры, вращение которой образует кольцо, на длину окружности, описываемой центром тяжести фигуры вокруг оси вращения, т. е.

V = F2πR, (4.3)

где F - площадь трапеции AA₁ N₁ N;

R - расстояние от оси вращения OO₁ до центра тяжести трапеции, который расположен на линии, соединяющей середины оснований трапеции на расстоя­нии h_c (по перпендикуляру) от ее большого основания. Из теоретической механики известно, что

Где b₂ - максимальная ширина выходной щели, м; b₁ - минимальная ширина выходной щели, м.

Как видно из рис. 4.3,

Подставив в уравнение (4.3) найденное значение F, получим