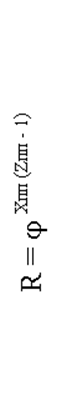Реферат: Расчет коробки скоростей

При выборе данного варианта соблюдаются условия:

- Число передач в группе 2.

- Основная и переборная группа имеют одинаковое число ступеней равное 2.

- Характеристики групп возрастают по мере приближения к шпинделю

(Х₀ = 1 – основная группа, Х₂ = 2 –первая переборная группа, Х₃ = 3 – вторая переборная группа)

Кинематическая схема для выбранного варианта структурной формулы приведена на рис. 1.

030501.080602.041.000 ПЗ Лист Изм Лист № документа Подпись Дата

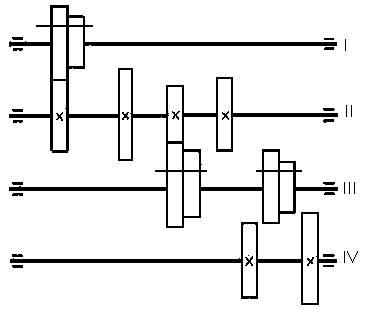
рис. 1

6. Построение структурной сетки

Структурная сетка дает представление о количестве передач между валами, знаменателе и диапазоне регулирования элементарных коробок, последовательности включения передач для обеспечения ряда частот вращения шпинделя. Структурная сетка характеризует закономерности изменения передаточных отношений в групповых передачах при изменении частот вращения шпинделя по геометрическому ряду.

Число валов в коробке равно (m+1), соответственно

030501.080602.041.000 ПЗ Лист Изм Лист № документа Подпись Дата

Структурная сетка строится в следующем порядке (см. рис. 3):

1). На чертеже в произвольном масштабе построим структурную сетку. Количество вертикальных прямых, равное (m +1), соответствует числу валов коробки, в нашем случае, при m = 3, число валов – четыре.

2). На равном расстоянии друг от друга наносим столь­ко горизонтальных прямых, сколько ступеней частот враще­ния имеет проектируемая коробка. В нашем случае, число ступеней равно 7 (рис. 2.).

3). Наносим на линии четвертого вала (без указания величин) точки n1 – n7,- изображающие частоты вращения шпинделя. Первый вал имеет одну частоту вращения, следовательно на вертикальной линии первого вала наносим исходную точку 0 симметрично относительно n_min = n₁ и n_max = n₇ , на уровне n₄ .

4). Первая группа состоит из двух передач, поэтому из точки О проводим два луча, при этом первому множителю 2₁ соответствует характеристика х = 1, т.е. на вертикальной линии вала на структурной сетке рас­стояние между точками 1 – 2 равно одному интервалу Для следующего множителя 2₂ характеристика х = 2, а расстояние между точками 3 – 5 и 4 – 6 равно двум интервалам, для множителя 2₃ характеристика равна х = 3 и расстояние между n₁ – n₄ , n₂ – n₅ , n₃ – n_6, n₄ – n₇ равно трем интервалам.

5). Полученные точки соединяем лучами.

7. Анализ структурной сетки

7.1. Симметричность и веерообразность расположения лучей.

Структурная сетка симметрична в пределах каждой группы.

7.2. Проверка оптимальности выбранного варианта сетки по диапазону регулирования.

R = j^{Хпп ( Z пп -1)} ,

где Zпп– число передач (ступеней) последней переборной коробки. В примере Zпп (Z₂ ) равно 2. Хпп – характеристика последней переборной коробки (х_пп =3).

Условие оптимальности R£ [R], где [R] = 8

В примере R = 1,26 ^3(2-1) = 2 < 8

Все условия соблюдены, следовательно выбранный вариант структуры можно считать оптимальным.

030501.080602.041.000 ПЗ Лист Изм Лист № документа Подпись Дата

n7

I II III IV

	n6
6	n5
0 2	5	n4
1	4	n3
3	n2

n1

Х = 1 Х = 2 Х = 3 030501.080602.041.000 ПЗ Лист Изм Лист № документа Подпись Дата

8. Построение структурного графика (графика частот вращения)

График частот вращения (структурный график) (рис. 4) является видоизмененной струк­турной сеткой. Он показывает действительные значения част­ных передаточных отношений передач и частот вращения валов.

Для построения графика частот вращения необходимо рассчитать числа оборотов шпинделя по формуле

n_i = n _min × j^n-1

Для нашего примера при j = 1,26

n ₁ = n_min = 125 об\мин

n ₂ = n_min × j ¹ = 157,5 об\мин n ₅ = n_min × j ⁴ = 315,06 об\мин

n ₃ = n_min × j ² = 198,45 об\мин n ₆ = n_min × j ⁵ = 396,97 об\мин

n ₄ = n_min × j ³ = 250,05 об\мин n ₇ = n_min × j ⁶ = 500,19 об\мин

Принимаем в соответствии с нормальными рядами чисел в станкостроении следующие значения чисел оборотов шпинделя:

n ₁ = n_min = 125 об\мин