Реферат: Расчет надежности, готовности и ремонтопригодности технических средств и вычислительных комплексов

(2.7)

причем .

Тогда для вычисления предела достаточно в функции , определяемую выражением (2.7), подставить s=0. Из (2.6) и (2.7) следует:

(2.8)

Так как , то

(2.9)

Это соотношение может быть весьма полезным при определении наработки на отказ или среднего времени восстановления системы.Для получения одного из этих показателей нет необходимости решать систему уравнений типа массового обслуживания. Достаточно лишь вычислить свободные члены и в выражении (2.7). В дальнейшем будет показано, что и модут быть получены непосредственно из графа состояний системы.

Коэффициент готовности, ялвляясь финальной вероятностью, не зависит от выбора начальных условий. Начальные условия определяют лишь переходные процессы в системе массового обслуживания типа система-ремонтоное предприятие. Это следует иметь в виду при составлении и решении уравнений функционирования системы. Вычислять коэффициент готовности целесообразно при таких начальных условиях, при которых достигается наибольшая простота раскрытия определителей.

Решение большого количества прикладных задач показывает , что переходные процессы в системах массового обслуживания, применительно к задачам надежности вычислительных систем обшего назначения, практически заканчиваются уже после двух-трех восстановлений. Поэтому часто на практике не интересуются функцией готовности, а за основу количественную характеристик надежности принимают коэффициент готовности.

Наработка на отказ является математическим ожиданием времени между соседними отказами восстанавливаемой системы. Эта характеристика мажет быть вычислена из соотношения:

(2.10)

где - вероятность того, что в течение времени t, отсчитанного от момента начала работы системы после i-го ее восстановления, не возникает отказ всей системы, т.е. , где - время между началом работы устройства после i-ого восстановления и (i+1)-м отказом. Вероятность может быть определена из системы уравнений функционирования системы.

Для определения наработки на отказ нет необходимости вычислять и интегрировать в соответствии с выражением (2.10). Достаточно найти преобразование Лапласа вероятности . Так как по определению

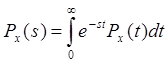, то

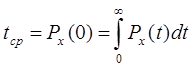(2.11)

Из последнего выражения видно, что для получения наработки на отказ достаточно найти, как и в случае вычисления среднего времени безотказной работы, преобразование Лапласа суммы вероятностей исправных состояний системы и положить в полученном выражении s=0, Отличие состоит лишь в том, что вероятность определяется при начальных условиях, отличных от начальных уловий , при которых определяется вероятность в выражении (2.3).

Описанный выше способ определения наработки на отказ применим лишь для частного случая, когда система имеет лишь одно отказовое состояние. В большинстве же практических случаев таких состояний много. Так же практических случаев таких состояний много. Так например при эксплуатации нерезервированной системы , состоянщей из N элементов, можно получить N отказовых состояний (Рис.2.1). В таких случаях определлить из уравнений функционирования системы затруднительно. Это объясняется тем, что неизвестно, при каких начальных условиях следует определять , так как предотказовых состояний может быть несколько, так как предотказовых состояний может быть несколько.

В ряде случаев удается найти наработку на отказ, воспользовавшись общей формулой для коэффициента готовности

(2.12)

Пользоваться этой формулой на практике целесообразно в следующих случаях:

1. среднее время восстановления системы известно из опыта;
2. система имеет лишь одно отказовое состояние, причем из этого состояния в соседние возможен переход с одной и той же интенсивностью 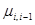. Тогда ;
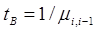3. система имеет несколько отказовых состояний, но интенсивности переходов из этих состояний в соседние одинаковы. Тогда среднее время восстановления системы равно, как в прежнем случае, .

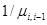Случаи 2 и 3 легко распознаются по графу состояний. Тогда для определения наработки на отказ достаточно найти описанным ранее способом.

На практике наиболее часто встречаются случаи, когда число отказовых состояний, системы велико, а значения интенсивностей восстановления зависят от отказового состояния. Тогда среднее время восстановления системы неизвестно, а наработку на отказ невозможно определить непосредственно по формуле (2.12).

Покажем, что среднее время восстановления и наработку на отказ мажно определить, если известны финальные вероятности пребывания системы во всех возможных состояниях и интенсивности переходов из отказовых в предотказвые состояния.

Интенсивность восстановления системы равна сумме произведений интенсивностей переходов из отказовых состояний в исправные на соответствующие вероятности отказвых состояний, т.е.

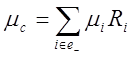(2.13)

где - вероятность того, что если система откажет, то она попадет в i-е отказовое состояние; - сумма интенсивностей переходов из i-го откаового состояния во все исправные состояния, граничащие с i-м отказовым состоянием; - подмоножество отказовых состояний, граничащих с исправными.

Вероятность легко вычислить по формуле

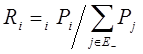(2.14)

где -финальная вероятность пребывания системы в i-м отказовом состоянии, граничащем с исправным; - финальная вероятность пребывания в j-м отказовом состоянии, граничащем или не граничащем с исправным состоянием; -подмножество всех отказовых состояний.