Реферат: Расчет прочности центрально растянутых предварительно напряженных элементов

С_д равно: при кратковременной нагрузке 1, при длительной нагрузке 1,5.

Ширина раскрытия трещин от длительной нагрузки по формуле при k=l,2 равна =

Приращение ширины раскрытия трещин от кратковременной нагрузки: =0,07 мм;

3.2. Расчет внецентренно-растянутых элементов

Площадь сечения арматуры А, расположенной ближе к линии действия силы N, обозначают F_a , а арматуры. А¢, удаленной от силы, — F_а ¢ . Характер работы внецентренно-растянутых элементов под нагрузкой зависит от эксцентрицитета е₀ . Если сила приложена между центрами тяжести сечений арматуры А к А¢ (для прямоугольного сечения, когда ), то имеем случай малых эксцентрицитетов. При малых эксцентрицитетах трещины пронизывают бетонное сечение элемента еще при относительно небольшой нагрузке; после этого продолжает работу только арматура (рис. 3, а). Несущая способность элемента оказывается исчерпанной при достижении арматурой предельных напряжений.

Условия прочности получим, составив уравнения моментов относительно центров тяжести сечений арматуры А и А¢: , (.6) где ; , (7) здесь .

При подборе сечений арматуры из условия определяют (8), а из условия — (9)

Если растягивающая сила N приложена вне расстояния между центрами тяжести арматуры А и А¢ :[для прямоугольного сечения, когда ], имеем случай больших эксцентрицитетов.

Характер работы внецентренно-растянутых элементов при больших эксцентрицитетах подобен.работе внецентренно-сжатых элементов с большими эксцентрицитетами: часть сечения сжата, а часть растянута (рис.6); высота сжатой зоны (для прямоугольного сечения) ограничивается условием . Предельную относительную высоту сжатой зоны определяют по формуле .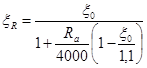

Разрушение сечения наступает, когда напряжения в арматуре А, а затем в бетоне сжатой зоны и в арматуре А¢ достигают предельных значений (для расчета — расчетных сопротивлений).

Проектируя все силы на ось элемента, получаем (10)

Уравнение моментов относительно центра тяжести арматуры А имеет вид (11)

Сравнив выражения (10) и (11) с, и устанавливаем, что условия прочности имеют тот же вид, что и при внецентренном сжатии, меняется только знак у силы N (растяжение вместо сжатия).

Прочность элемента проверяют по условий (11), предварительно определив высоту сжатой зоны х из формулы (10). Если , то в условии (11) принимают .

Прочность внецентренно-растянутых элементов по наклонному сечению рассчитывают так же, как проч­ность изгибаемых элементов, но поскольку растягивающая сила N способствует более раннему образованию косых трещин и уменьшает усилие , воспринимаемое бетоном сжатой зоны в наклонном сечении, в формулы и вводят понижающий коэффициент :, но не менее 0,2. (12)

Расчет внецентренно-растянутых элементов на образование трещин аналогичен рассмотренному выше расчету изгибаемых и внецентренно-сжатых элементов и состоит в проверке условия

Из рис. 4 видно, что . (13)

Величины , и определяют по формулам, изгибаемых железобетонных элементов.

Ширину раскрытия трещин при определяют по формуле при k=1,2 и напряжениях в арматуре А: ; (14) —см. рис. 4; если сила приложена между арматурой А и А', величину в формуле (14) принимают со знаком минус. Величину определяют по формулам сжатых железобетонных элементов в формуле перед вторым членом меняется знак. Когда , принимают .

Расчет прогибов внецентренно-растянутых элементов полностью подобен расчету сжатых железобетонных элементов, прогибов внецентренно-сжатых элементов, но в формуле кривизны перед вторым членом, выражающим кривизну от силы N, знак минус меняется на плюс, поскольку и от заменяющего момента , и от силы N кривизны имеют один знак.

4. Преварительно напряженные железобетонные конструкции

4.1 Расчет центрально-растянутых преварительно-напряженных элементов.

Рассмотрим последовательное изменение напряженно-деформированного состояния центрально-растянутого предварительно-напряженного элемента изготовляемого с натяжением арматуры на упоры (рис. 12). Площадь сечения бетона , площадь сечения напрягаемой арматуры .

Состояние I. Уложенная в форму арматура натянута до

напряжений .

Состояние II. Элемент забетонирован. Арматура удерживается в напряженном состоянии упорами, но в ней произошли первые потери напряжений и напряжения стали равны .

Состояние III. Бетон набрал необходимую прочность. Арматура отпущена с упоров. Вследствие сцепления между арматурой и бетоном произошло обжатие бетона до напряжений . Элемент укоротился. Бетон и арматура получили одинаковую деформацию, т. е..

Напряжения в арматуре в результате обжатия элемента уменьшились на .

Таким образом, напряжения в арматуре равны