Математика / Реферат: Равногранный тетраэдр

Реферат: Равногранный тетраэдр

Т.к. трёхгранный угол однозначно определяется своими тремя плоскими углами, то сдедующие доказательства будут аналогичны предудущему.

Дальше можно рассуждать по следующей схеме: (4)=>(5)=>(6)=>(1) (откуда уже следует равносильность первых шести условий).

Докажем (4)=>(5).

    Из условия следует, что углы ADB=ACB, ADC=ABC, BDC=BAC. Тогда треугольники ABC, ADC, ADB, BCD подобны, но треугольники ADB и DAC имеют общую сторону, т.е. они равны, аналогично равны екжду собой и остальные треугольники, т.е. тетраэдр – равногранный.

Докажем (5)=>(6).

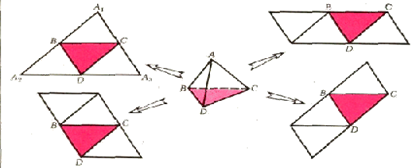    Разрежем тетраэдр АВСD по рёбрам АВ, АС, АD и рассмотрим развёртку А1 ВА2 DА3 С (рис. => ), тогда в точках В, С и D приложены по три угла, сумма которых 180°, поэтому углы А1 ВА2 , А2 ОА3 , А3 СА1 — развер­нутые; значит, А1 А2 А3 — треугольник, содержащий точки В, С, D и являющийся разверткой тетраэдра АВСD, Для остальных разверток рассуждение аналогично.

Докажем (6)=>(1).

    Посмотрев на рисунок можно увидеть, что на развёртке (например треугольник) скрещивающиеся рёбра являются противоположными сторонами параллелограмма, т.е. они равны.

Наш следующий шаг - доказательство равносильности (1)<=>(7).

Докажем (1)<=>(7).

В самом деле, поскольку скрещиваю­щиеся ребра тетраэдра — диагонали граней описанного параллелепипеда, из попарного равенства ребер следует, что грани опи­санного параллелепипеда — прямо­угольники и наоборот.

Теперь мы предлагаем рассуж­дать по схеме (7)=>(8)=>(9)=>(10)=>(7).

Докажем (7)=>(8).

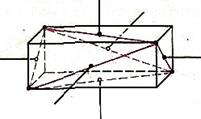
    Взглянув на (рис. =>), вы легко уста­новите, что осями симметрии явля­ются прямые, соединяющие центры симметрии противоположных граней описанного (прямоугольного) парал­лелепипеда, или, что здесь то же са­мое, общими перпендикулярами скре­щивающихся рёбер.

Докажем (8)=>(9).

    Общими перпендикулярами скрещивающихся рёбер являются отрезки соединяющие середины противоположных граней описанного параллелограмма (прямоугольного) (рис. ^), а это значит, что эти отрезки попарно перпендикулярны (т.к. каждый из отрезков перпендикулярен граням, которые он соединяет).

Докажем (9)=>(10).

    Отрезки, соединяющие середины скрещивающихся рёбер – перпендикулярны, но это и есть средние линии.

Докажем (10)=>(7).

Следующая цепочка рассуждений (0)=>(11),(12),(13),(14),(15). Мы докажем, что (11)=>(1), (12)=>(3), (13)=>(12), (14)=>(1), (4)=>(15); тем самым будет установлена равносильность первых 15 свойств.

Докажем (11)=>(1).

    Запишем условие (11) в виде a2 +b2 +c2 (1) =a2 +b1 +c1 (2) =b2 +a1 +c1 (3) =c2 +a1 +b1 (4) , где a1 b1 c1 – длины рёбер тетраэдра, исходящих из одной вершины, a2 b2 c2 – длины соответственно скрещивающихся с ними рёбер. (1)-(2)=(3)-(4) или b2 +c2 -b1 -c1 =b2 +c1 -c2 -b1 , т.е. 2с2 =2с1 или по-другому с2 =с1 , рассуждая аналогично для a1 ,a2 ,b1 ,b2 , получаем a1 =a2 , b1 =b2 , c1 =c2 , а это и есть запись условия (1).

Докажем (12)=>(3).

    Для этого утверждения предварительно заметим, что S4 =S1 c14 +S2 c24 +S3 c34 (**), где Si - площади i-й грани, а сij – косинус двугранного угла между i-й и j-й гранью. Соотношение (**) сразу следует из теоремы о площади проекции, если спроектировать все грани тетраэдра на четвёртую грань. Написав ещё три таких соотношения (для трёх других граней) и воспользовавшись условием (12), приходим к системе с14 +с24 +с34 =с13 +с23 +с34 =с12 +с23 +с24 =с12 +с13 +с14 , которая решается точно так же как система из предыдущего утверждения. Получим с14 =с23 , с24 =с14 , с34 =с12 , откуда следует равенство соответствующих углов, т.е. (3).

Докажем (13)=>(12).

    Утверждение очевидно следует из формулы для объёма тетраэдра V=Sh/3: S1 h1 /3=S2 h2 /3=S3 h3 =S4 h4 /3 S1 =S2 =S3 =S4 по условию => h1 =h2 =h3 =h4 .

Докажем (14)=>(1).

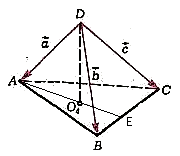
    Обозначим через Оi центр тяжести i-й грани и выразим |DO4 | через стороны /DA/=/a/, /DB/=/b/, /DC/=/c/ (рис. =>). /DO4 / = =/DA/ + + /AO4 / = /DA/ + 2/3*/AE/ = /DA/ + 2/3*1/2*(/AB/ + /AC/) = = 1/3*(/DA/ + /AB/) + 1/3*(/DA/ + /AC/) + 1/3*/DA/ = 1/3*/DA/ + + 1/3*/DB/ + 1/3*/DC/ = 1/3*(/a/+/b/+/c/). Отсюда находим скалярный квадрат вектора /DO4 / : (DO4 )2 =1/9*(a2 +b2 +c2 +2/a/*/b/+2/a/*/c/+2/b/*/c/). Обозначив a1 =|a|, b1 =|b|, c1 =|c|, a2 =|BC|, b2 =|AC|, c2 =|AB| и воспользовавшись тем, что /AB/=/b/-/a/, /BC/=/c/-/b/, /CA/=/a/-/c/, можно DO4 выразить в виде ( DO4 )2 = 1/3*(( a1 )2 +( b1 )2 +( c1 )2 ) + 1/9*(( a2 )2 +( b2 )2 +( c2 )2 ) .

Напишем ещё три таких соотношения для трёх остальных граней:

(DO3 )2 =1/3*((a2 )2 +(b2 )2 +(c1 )2 ) + 1/9*((a1 )2 +(b1 )2 +(c2 )2 );

(DO2 )2 =1/3*((a2 )2 +(b1 )2 +(c2 )2 ) + 1/9*((a1 )2 +(b2 )2 +(c1 )2 );

(DO1 )2 =1/3*((a1 )2 +(b2 )2 +(c2 )2 ) + 1/9*((a2 )2 +(b1 )2 +(c1 )2 ).

По условию DO1 =DO2 =DO3 =DO4 приравняем, например, DO1 =DO2 , получаем :

1/3*((a1 )2 +(b2 )2 +(c2 )2 ) + 1/9*((a2 )2 +(b1 )2 +(c1 )2 ) = 1/3*((a2 )2 +(b1 )2 +(c2 )2 ) + 1/9*((a1 )2 +(b2 )2 +(c1 )2 ),

1/3*(a1 )2 + 1/3*(b2 )2 + 1/9*(a2 )2 + 1/9*(b1 )2 = 1/3*(a2 )2 + 1/3*(b1 )2 + 1/9*(a1 )2 + 1/9*(b2 )2 ,

2/9*(a1 )2 + 2/9*(b2 )2 = 2/9*(a2 )2 + 2/9*(b1 )2 ,

(a1 )2 + (b2 )2 = (a2 )2 + (b1 )2 (***),

Приравняв DO3 =DO4 , получаем :

1/3*((a2 )2 +(b2 )2 +(c1 )2 ) + 1/9*((a1 )2 +(b1 )2 +(c2 )2 ) = 1/3*((a1 )2 +(b1 )2 +(c1 )2 ) + 1/9*((a2 )2 +(b2 )2 +(c2 )2 ),

К-во Просмотров: 514
Бесплатно скачать Реферат: Равногранный тетраэдр