Реферат: Разделение каналов в радиолинии
При этом сигналы должны удовлетворять определенным условиям. Пусть ![]() - множество канальных сигналов к-го канала. Назовем
- множество канальных сигналов к-го канала. Назовем ![]() - линейно разделимыми множествами, если для них справедливо выражение ( 9).
- линейно разделимыми множествами, если для них справедливо выражение ( 9).
Теорема: Для того, чтобы множества ![]() были линейно разделимыми, необходимо и достаточно, чтобы они удовлетворяли условию линейной независимости. Условием линейной независимости сигналов (функций) определенных на отрезке
были линейно разделимыми, необходимо и достаточно, чтобы они удовлетворяли условию линейной независимости. Условием линейной независимости сигналов (функций) определенных на отрезке ![]() является невозможность тождества:
является невозможность тождества:
![]() ( 10)
( 10)
при любых значениях коэффициентов ![]() ,
,![]() ,…,
,…,![]() , кроме случая
, кроме случая ![]() . Если окажется, что можно подобрать коэффициенты
. Если окажется, что можно подобрать коэффициенты ![]() ,
,![]() ,…,
,…,![]() , при которых удовлетворяется соотношение ( 10), то сигналы станут линейно зависимыми и неразделимыми. К линейно независимым сигналам относятся сигналы вида:
, при которых удовлетворяется соотношение ( 10), то сигналы станут линейно зависимыми и неразделимыми. К линейно независимым сигналам относятся сигналы вида:
 ( 11)
( 11)
где ![]() и
и ![]() - вещественные числа. В общем случае критерий линейной независимости функций
- вещественные числа. В общем случае критерий линейной независимости функций ![]() , определенных на интервале
, определенных на интервале ![]() дается теоремой Грама: Для того, чтобы функции
дается теоремой Грама: Для того, чтобы функции ![]() были линейно независимыми, необходимо и достаточно, чтобы был отличен от нуля определитель матрицы
были линейно независимыми, необходимо и достаточно, чтобы был отличен от нуля определитель матрицы ![]() , элементы которой определяются соотношением:
, элементы которой определяются соотношением:
 . ( 12)
. ( 12)
Т.е. условие линейной независимости функций можно записать в следующей форме:
 , ( 13)
, ( 13)
где G – определитель Грама. Определитель Грама всегда не равен нулю для ортогональных функций, которые удовлетворяют условию:
![]()
![]()
 ( 14)
( 14)
где ![]() - весовая функция. Согласно теории функции действительного переменного систему линейно независимых функций можно свести к некоторой ортогональной системе функций. Использование как правило в качестве канальных сигналов системы ортогональных функций связано с тем обстоятельством, что разделение этих сигналов осуществляется без ухудшения отношения сигнал - шум.
- весовая функция. Согласно теории функции действительного переменного систему линейно независимых функций можно свести к некоторой ортогональной системе функций. Использование как правило в качестве канальных сигналов системы ортогональных функций связано с тем обстоятельством, что разделение этих сигналов осуществляется без ухудшения отношения сигнал - шум.
3 Разделение сигнала по форме
При разделении сигналов по форме базисные функции ![]() должны быть линейно независимыми и ортогональными. При этом передаваемая информация заключается в амплитуде базисных функций. В случае разделения по форме канальный сигнал имеет вид:
должны быть линейно независимыми и ортогональными. При этом передаваемая информация заключается в амплитуде базисных функций. В случае разделения по форме канальный сигнал имеет вид:
![]() , ( 15)
, ( 15)
где ![]() - период канального сигнала,
- период канального сигнала, ![]() - отсчеты первичного сигнала.
- отсчеты первичного сигнала.
Выражение справедливо в случае, когда информация заключена в амплитуде сигнала. В качестве базиса используются функции, удобные с точки зрения технической реализации. В частности полиномы Лежандра, Матье и др. При использовании полиномов Лежандра отдельные базисные функции равны:
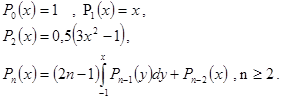 ( 16)
( 16)
Условие ортогональности в этом случае имеет вид:
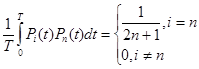 ( 17)
( 17)
Т.о., средняя мощность каждого ортогонального колебания равна (![]() ). Для того чтобы выровнять мощность канальных сигналов на передающей стороне каждую базисную функцию умножают на
). Для того чтобы выровнять мощность канальных сигналов на передающей стороне каждую базисную функцию умножают на ![]() .
.
При использовании нечетных полиномов в сигнале появляются скачки, для передачи которых потребуется широкая полоса радиоканала (рисунок 3).

Рисунок 3
Для устранения этого недостатка в передаваемом сигнале у нечетных полиномов через период изменяют полярность (рисунок 4).
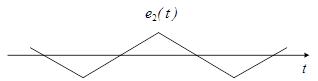
Рисунок 4
Рассмотрим структурную схему передающей части системы с ортогональными сигналами (рисунок 5).
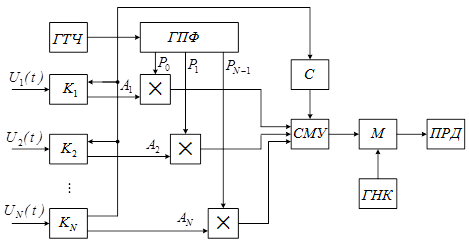
Рисунок 5
где СМУ – суммарно-масштабирующий усилитель, ГПФ – генератор полиномиальных функций, ГТЧ – генератор тактовой частоты, ГНК – генератор несущего колебания, К – ключ, С – синхронизатор.
Первичный сигнал ![]() - непрерывная функция времени. ГТЧ формирует кратковременный импульс с частотой
- непрерывная функция времени. ГТЧ формирует кратковременный импульс с частотой ![]() . Ключ К хранит значение отсчетов за весь период, а синхронизатор формирует синхросигнал.
. Ключ К хранит значение отсчетов за весь период, а синхронизатор формирует синхросигнал.
Тогда групповой будет сигнал представлен в следующем виде:
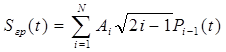 ,
, ![]() , ( 18)
, ( 18)
Для разделения канальных сигналов используют свойство их ортогональности. Эта операция сводится к вычислению скалярного произведения группового сигнала на базисную функцию выделяемого канала
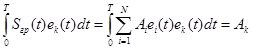 ( 19)
( 19)
Структурная схема приемной части системы приведена на рисунке 6.
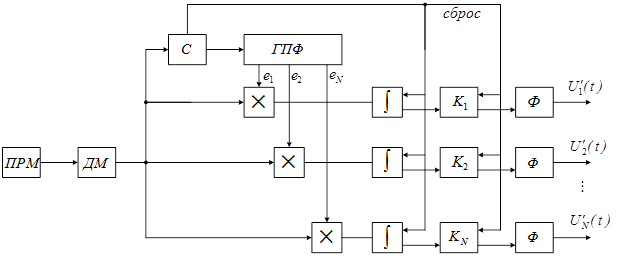
Рисунок 6
Ортогональные полиномы Лежандра, Чебышева и т.д. являются непрерывными аналоговыми сигналами и, следовательно, устройствам их генерирования и обработки свойственны недостатки присущие всем аналоговым устройствам:
- невозможность унификации и стандартизации большинства устройств;
- высокие требования к температурной стабильности;
- сложность технической реализации генераторов полиномиальных функций.
Поэтому в настоящее время в качестве канальных сигналов используются различные типы цифровых сигналов, в частности ансамбль функций Уолша.
4 Частотное разделение каналов (ЧРК)
ЧРК – частный случай разделения ортогональных сигналов. Базисные функции ортогональны в частотной области. Вид базисных функций:
![]() , ( 20)
, ( 20)