Реферат: Разложимые показатели расслоения

Условие 7 (передачи) . От расщепления какой-либо группы, задаваемой F , на две, например, F₁ и F₂ (или более) групп функция J(F) ³ max[J(F₁ ),J(F₂ )] .

По сути, последнее условие мало добавляет к уже приведенным условиям повторения и монотонности, так как уточнилась лишь формулировка - появился функционал от смеси двух аргументов, вместо функционала от одного. В самом деле функции распределения F ₁ иF ₂ присутствуют и в правой и в левой частях неравенства, так как функция F= l F₁ +(1 -l )F₂ , где l Î [0,1} и F ₁ ¹ F ₂ . Возникает вопрос, нельзя ли функционал от смеси двух аргументов представить в виде смеси функционалов от каждого. Такое представление полезно из-за возможности сильно облегчить расчет, который такое оно позволило бы осуществить. Однако последнее высказывание относится уже не только к свойствам расслоения и его показателей, а скорее к методу расчета самого показателя расслоения.

Действительно, если речь идет о стране, состоящей из ряда районов, то для расчета меры неравенства в ней после уже сделанных расчетов коэффициентов расслоения в каждом районе необходимо знать функцию распределения F для всей страны, хотя она - смесь функций распределения F_i для каждого района i . Для этого следует передать из всех районов доходы всех людей, из совокупности которых получается функция F для всей страны. А можно ли ограничиться только “сжатой” информацией, например, о средних доходах в районах, самих мерах расслоения и еще о чем-либо? Примеры, показывающие такую возможность, имеются - это так называемые неразложимые смеси функций распределения и достаточные статистики для последних.

Свойство восстановления расслоения всего общества по смеси расслоений в его группах очевидно, поэтому очень полезно иметь и возможность пересчета функционалов (мер неравенства) от смеси по “сжатым” данным о коэффициентах расслоения в отдельных частях. Отсюда появляется следующее предположение о способе пересчета.

Условие 8 (разложимости) . Функционал J(F) может считаться разложимым в том случае, когда он имеет вид J(F)=[ m (F_i )]J(F_i )+J(F₀ ) , где p[ m (F_i )] -весовая функция, зависящая от центров m (F_i ) групп i, (i=) и, кроме того, F_i -функции распределения доходов в группах, а F₀ - функция распределения центров групп, число которых m .

2. Показатели расслоения

Условие разложимости - это определение разложимого функционала J : функционал J называется разложимым, когда он, после подходящего монотонного преобразования, может быть представлена в виде уже приведенной суммы, где F₀ - смесь функций распределения F_i в группах . В этом определении сразу дано такое представление функции J , которое могло бы быть дано в два этапа, первый - определение разложимости как некоторой зависимости от функций распределения в группах и на их центрах, и второй - приведение к аддитивной зависимости после монотонного преобразования. Если далее определить показатель (или меру) расслоения (или неравенства) I как разложимый функционал J , удовлетворяющую условиям 1-7, то может быть доказана следующая теорема.

Теорема . Непрерывно дважды дифференцируемая разложимая мера расслоения удовлетворяет условиям передачи и однородности тогда и только тогда, кода она имеет вид

для некоторого a ³ 0, где m (F) - центр распределения F , а w_a ( x ) - решение уравнения x ( d ² w ( x )/ dx ² )+(1- a )( dw / dx )= b .

Если учесть, что решения w(x) дифференциального уравнения xw”+(1 -a)w’=b и соответствующие им p(F_l ) имеют вид

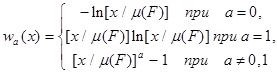иp_a (F_l )=[l/ m (F)]^a ,

то общим видом показателя расслоения будет следующий

.

Смешивающая функция для дискретных величин F ₀ ( l ) в точке l = m ( F_i ) имеет скачёк величины l _i , для непрерывного случая аналогично.

Результат теоремы состоит, во-первых, в том, что мера расслоения не зависит от численности общества (или групп), а зависит лишь от функции распределения. Во-вторых, характеристических (существенных) свойств всего два - однородности и передачи.

Все остальные следуют из них. Таким образом, не было необходимости приводить и описывать все свойства расслоения, хотя они многое проясняют. Более того теорема показывает, что меру расслоения можно искать в виде и функция w(x) связана с множеством решений уравнения xw”(x)+(1 -a)w’(x)=b .

3. Частные показатели

Осталось привести лишь частные случаи. При a =0 имеем

I ( F )= ,

при a=1 получается мера расслоения Тайла (Theil):

I(F)= ,

наконец, при a=2 имеем квадрат коэффициента вариации:

I(F)= ,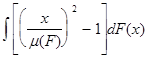

множители перед интегралом опущены в соответствии с определением разложимости.

Рассмотрим общество, заданное функцией распределения F , состоящее из m групп, каждая из которых определяется своей функцией распределения F_i (). В этом случае F= , где l _i ³ 0 , и Sl _i = 1. Кроме того, чтобы F была функцией распределения всего общества необходимо представление распределения центров групп в виде F₀ (x)= S_i H(x -x_i ) l _i , где H(x) - функция Хевисайда, т.е. она равна 1 при x ³ 0 и 0 в других случаях, а l _i =n_i /n и x_i = m (F_i ) .

Остается привести лишь разложения уже приведенных показателей расслоения.

Для первого показателя - логарифмической меры расслоения - имеем функцию w(x) =-ln[x/ m (F)] , которая дает название меры. Для нее весовая функция p имеет вид p[ m (F_i )]=1 . а показатель расслоения

I[ m (F)]= ,

или, в более общем виде для распределения F(x)= , где F(x/l)=F_i (x) при l= m ( F_i ) ,

.
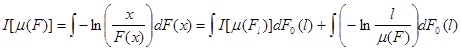