Реферат: Разработка алгоритмов и программ выполнения операций над последовательными и связанными представлениями структур данных

F =

K=1

Где

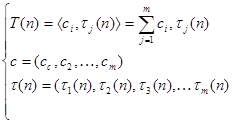
В моём случае T(NX,NY,NZ)=O(NX*(NY+NZ) =>

T(NX,NY,NZ)=C1*NX*(NY+NZ)+C2*(NY+NZ)+C3*(NY)+C4*(NZ)

Следовательно для моего примера мы получим:

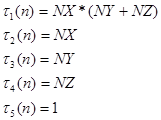
Для того чтобы получить значение функции на K- том эксперименте, мы засекаем значение времени перед вызовом функции, которая реализует алгоритм, вставим оператор вида:

TikTak=clock();

Где функция clock() даёт время с точностью до нескольких миллисекунд (в языке С++ она описана в заголовочном файле time.h) . После выполнения процедуры, реализует алгоритм, мы находим разность времени

TikTak=cloc() - TikTak;

После всех проделанных манипуляций нужно прировнять к нулю все частные производные. Это будет выглядеть, в общем виде, примерно так:

После раскрытия скобок и замены T(n)= T(n)=(c, t (n))= получим

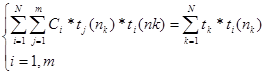
Положим А ij=(ti, tj) и B=(ti,TikTak) = > мы получили систему уравнений AX=B , где Х=С. Формирование в матрице столбцов А и столбцов В записывается очень легко используя любой алгоритмический язык. После заполнения матрицы её остаётся решить и вывести решения этой задачи. Решение производиться методом Жордана.

Априорная временная оценка процедур.

Процедура вывода графа на экран в последовательном представлении:

Void prin3(Array *X, int N1, int N)

X – граф в связаном представлении

N – количество вершин графа.

N1 – количество дуг в графе Х

O(N,N1)=N*N1

Процедура вывода графа на экран в связаном представлении:

Void print3(Spisok **X, int N)

X – граф в связаном представлении

N – количество дуг в графе.

O(N)=N

Процедура вычисления разности графов с возвращающим значением последовательного графа:

Array * RaznostZ(int n, int &n1, Array *X, Spisok **Y,Array *Z)

N - количество дуг графа

N1 – количество вершин в графе Х

X – грав в последовательном представлении

Y - грав в связаном представлении

Z – грав в последовательном представлении

O(N,N1)=N1*N*k=N1*N2