Реферат: Разработка библиотечных средств

Наследование

Наследование в ООП позволяет классу получать совйства другого класса объектов. Родительский класс служит шаблоном для производного класса; этот шаблон можно менять различными способами. Наследование является важным положением, поскольку оно позволяет повторно использовать определение класса без значительных изменений в коде.

Полиморфизм

Строится на описаной выше концепции наследования. Программа посылает одно и тоже сообщение как объекту родительского класса, так и всем объектам производных классов. И родительский класс, и классы-потомки ответят на сообщение соответствующим образом. Полиморфизм дает возможность дополнять уже существующие части программы.

Виртуальные функции

Виртуальные функции определяются в родительском классе, а в производных классах происходит доопределение этих функций и для них создаются новые реализации. При работе с виртуальными функциями сообщения передаются как указатели, которые указывают на объект вместо прямой передачи объекту. Виртуальные функции используют таблицу для адресной информации. Эта таблица инициализируется во время выполнения при помощи конструктора.

Конструктор вызывается каждый раз, когда создается объект его класса. Задача конструктора в данном случае состоит в связывании виртуальной функции с таблицей адресной информации. Во время компиляции адрес виртуальной функции неизвестен; вместо этого ей отводится позиция в таблице адресов. Эта позиция будет содержать адрес функции [5].

Глава 2. Задачи линейной алгебры

2.1. Вычисление определителей

Пусть имеем квадратную матрицу размером nґ n:

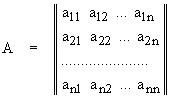. (2.1.1)

Требуется вычислить определитель матрицы det(A).

Эквивалентным преобразованием матрицы называют преобразования матрицы, не изменяющие величину определителя матрицы. Эквивалентным является следующее преобразование: любую строку матрицы можно заме-нить суммой исходной строки и любой другой, умноженной на любое число, не равное нулю.

Используя такого рода преобразования можно попытаться привести ис-ходную матрицу к треугольному виду:

,

при этом det(A) = det(Aў ).

Формула для пересчета элементов матрицы имеет вид:

, (2.1.2)

гдеi- номер столбца, в котором элементы, лежащие ниже главной
диагонали, превращаются в нули;

j- номер элемента в обрабатываемом столбце (т.е. номер строки);

k- номер элемента в текущей строке.

Алгоритм приведения матрицы к треугольному виду включает в себя 3 вложенных цикла:

- внешний цикл, i = 1 .. n-1 ;

- средний цикл, j = i+1 .. n ;

- внутренний цикл, k = i+1 .. n .

Теперь искомый определитель вычисляется как произведение диагональных элементов:

.

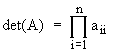Описанный выше алгоритм дает результат не всегда. Если при выполнении i-того шага внешнего цикла диагональный элемент aii оказывается равным нулю, а среди элементов i-того столбца с номерами от i+1 до n есть хотя бы один не нулевой, алгоритм завершается безрезультатно (из-за невозможности вычислений по формуле (2.1.2). Для того, чтобы это не происходило, используется прием, который называется “выбор главного элемента”.

При выполнении очередного шага цикла по i предварительно выполняются следующие операции: