Реферат: Разработка схемы электронного эквалайзера
Период дискретизации фильтра для определения порядка данного фильтра:
![]() мс.
мс.
Переходная функция ![]() :
:
![]() .
.
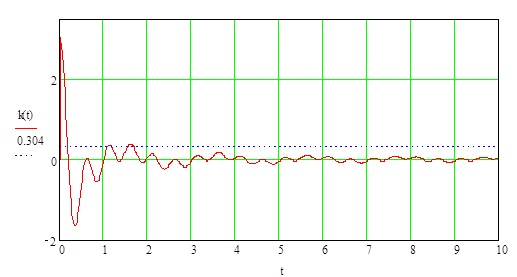
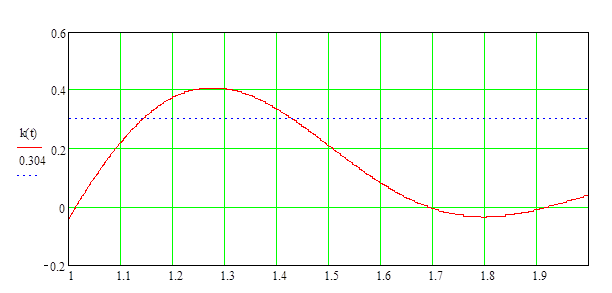
Рис.4. Переходная функция ПФ1.
![]()
![]()
![]()
Определим коэффициенты фильтра ПФ1:
Таблица 3.
| n | a | 27 | 0,050566544 |
| 0 | -0,027392762 | 28 | 0,009754081 |
| 1 | -0,049172612 | 29 | -0,011037791 |
| 2 | -0,057498995 | 30 | -0,001629017 |
| 3 | -0,049981285 | 31 | 0,033889051 |
| 4 | -0,031300945 | 32 | 0,077854621 |
| 5 | -0,011253529 | 33 | 0,106118285 |
| 6 | -0,000340822 | 34 | 0,098772242 |
| 7 | -0,004862821 | 35 | 0,049903812 |
| 8 | -0,023768747 | 36 | -0,028191457 |
| 9 | -0,048803001 | 37 | -0,108781867 |
| 10 | -0,068018861 | 38 | -0,161509497 |
| 11 | -0,071175102 | 39 | -0,166035038 |
| 12 | -0,054593763 | 40 | -0,122644307 |
| 13 | -0,023199651 | 41 | -0,054716469 |
| 14 | 0,011335417 | 42 | -0,001027688 |
| 15 | 0,035666075 | 43 | -9,11331E-05 |
| 16 | 0,040864762 | 44 | -0,072393216 |
| 17 | 0,026753627 | 45 | -0,207878004 |
| 18 | 0,002377281 | 46 | -0,36456585 |
| 19 | -0,017802566 | 47 | -0,480163419 |
| 20 | -0,020450558 | 48 | -0,493412799 |
| 21 | 0,000250373 | 49 | -0,367750032 |
| 22 | 0,039336231 | 50 | -0,108340337 |
| 23 | 0,082625786 | 51 | 0,234522697 |
| 24 | 0,112674731 | 52 | 0,57791205 |
| 25 | 0,116628962 | 53 | 0,831063217 |
| 26 | 0,09245668 | 54 | 0,924 |
Таким образом, получим 2*27+1=55.
Полосовой фильтр 2. (ПФ2)
Частоты среза фильтра: ![]() кГц,
кГц, ![]() кГц ;
кГц ;
![]() рад/с;
рад/с;
![]() рад/с;
рад/с;
Частота дискретизации fД =18 кГц;
Период дискретизации фильтра для определения порядка данного фильтра:
![]() мс.
мс.
Переходная функция ![]() :
:
![]() .
.


Рис.5. Переходная функция ПФ2.
![]()
![]()
![]()
Определим коэффициенты фильтра ПФ2:
Таблица 4.
| n | a | n | a | n | a | n | a |
| 0 | -0,011403272 | 26 | 0,008564942 | 51 | -0,008846573 | 76 | -0,18082 |
| 1 | -0,000671233 | 27 | 0,021102423 | 52 | 0,037595032 | 77 | -0,1784 |
| 2 | -0,002996937 | 28 | 0,004265003 | 53 | 0,080410875 | 78 | 0,095797 |
| 3 | -0,018770032 | 29 | -0,036469236 | 54 | 0,051282637 | 79 | 0,448421 |
| 4 | -0,022854085 | 30 | -0,056323545 | 55 | -0,042798877 | 80 | 0,481368 |
| 5 | 0,001126855 | 31 | -0,024681939 | 56 | -0,112227487 | 81 | 0,024559 |
| 6 | 0,034325515 | 32 | 0,032843223 | 57 | -0,083934873 | 82 | -0,58945 |
| 7 | 0,040979404 | 33 | 0,059807045 | 58 | 0,010970719 | 83 | -0,77512 |
| 8 | 0,011187719 | 34 | 0,033616102 | 59 | 0,072924662 | 84 | -0,27695 |
| 9 | -0,025443793 | 35 | -0,010193441 | 60 | 0,052722936 | 85 | 0,516062 |
| 10 | -0,033795035 | 36 | -0,024329191 | 61 | 0,004870193 | 86 | 0,897 |
| 11 | -0,013271274 | 37 | -0,007485342 | 62 | 0,006592027 | ||
| 12 | 0,005692888 | 38 | 0,000376818 | 63 | 0,047575263 | ||
| 13 | 0,002823747 | 39 | -0,022171202 | 64 | 0,039797492 | ||
| 14 | -0,007074135 | 40 | -0,043667715 | 65 | -0,056146793 | ||
| 15 | 0,002253171 | 41 | -0,019772772 | 66 | -0,152792284 | ||
| 16 | 0,028241957 | 42 | 0,041957097 | 67 | -0,123885355 | ||
| 17 | 0,037692296 | 43 | 0,079697904 | 68 | 0,034673544 | ||
| 18 | 0,008942625 | 44 | 0,047836289 | 69 | 0,175624872 | ||
| 19 | -0,035597973 | 45 | -0,025176686 | 70 | 0,159227505 | ||
| 20 | -0,051085442 | 46 | -0,066753777 | 71 | 0,017255804 | ||
| 21 | -0,02221679 | 47 | -0,044175408 | 72 | -0,085824627 | ||
| 22 | 0,01877206 | 48 | 0,001261156 | 73 | -0,058283491 | ||
| 23 | 0,031228765 | 49 | 0,012420123 | 74 | 0,003729665 | ||
| 24 | 0,013463011 | 50 | -0,008885547 | 75 | -0,047156433 | ||
| 25 | -0,000947481 |
Таким образом, получим: 2*N+1=87.
Полосовой фильтр 3. (ПФ3)
Частоты среза фильтра: ![]() кГц,
кГц, ![]() кГц ;
кГц ;
![]() рад/с;
рад/с;
![]() рад/с;
рад/с;
Частота дискретизации fД =18 кГц;
Период дискретизации фильтра для определения порядка данного фильтра:
![]() мс.
мс.
Переходная функция ![]() :
:
![]() .
.

Рис.6. Переходная функция ПФ3.
![]()
![]()
![]()
Определим коэффициенты фильтра ПФ3:
Таблица 5.
| n | a | n | a | n | a |
| 0 | 0,040797115 | 16 | -0,020022291 | 32 | 0,033266 |
| 1 | 0,001220133 | 17 | 0,055837751 | 33 | 0,260118 |
| 2 | 0,039978222 | 18 | 0,098343639 | 34 | -0,09252 |
| 3 | 0,02276506 | 19 | -0,121159876 | 35 | -0,25744 |
| 4 | -0,105348775 | 20 | -0,099106166 | 36 | 0,086745 |
| 5 | -0,016132812 | 21 | 0,105674587 | 37 | 0,060059 |
| 6 | 0,099578035 | 22 | 0,034090375 | 38 | 0,051138 |
| 7 | 0,000120154 | 23 | 0,00765609 | 39 | 0,204207 |
| 8 | -0,018054176 | 24 | 0,033408102 | 40 | -0,26949 |
| 9 | -0,004859298 | 25 | -0,15056655 | 41 | -0,34219 |
| 10 | -0,082884453 | 26 | -0,049309806 | 42 | 0,383098 |
| 11 | 0,033032806 | 27 | 0,20912763 | 43 | 0,239879 |
| 12 | 0,12739375 | 28 | 0,019199721 | 44 | -0,17655 |
| 13 | -0,050946367 | 29 | -0,114030202 | 45 | 0,0433 |
| 14 | -0,081052541 | 30 | 0,000617104 | 46 | -0,43205 |
| 15 | 0,02041495 | 31 | -0,089953059 | 47 | -0,30865 |
| 48 | 1,286545 | ||||
| 49 | 0,361651 | ||||
| 50 | -2,03978 | ||||
| 51 | -0,1583 | ||||
| 52 | 2,34 |
Таким образом, получим: 2*N+1=53
Полосовой фильтр №4 (ПФ4)
Частоты среза фильтра: ![]() кГц,
кГц, ![]() кГц ;
кГц ;
![]() рад/с;
рад/с;
![]() рад/с;
рад/с;
Частота дискретизации fД =18 кГц;
Период дискретизации фильтра для определения порядка данного фильтра:
![]() мс.
мс.
Переходная функция ![]() :
:
![]()


Рис.7. Переходная функция ПФ4.
![]()
![]()
![]()
Определим коэффициенты фильтра ПФ4:
Таблица 6.
| n | a | n | a |
| 0 | -0,039924801 | 13 | -0,14859 |
| 1 | -0,036859051 | 14 | -0,03612 |
| 2 | -0,030099957 | 15 | 0,339846 |
| 3 | 0,181767777 | 16 | -0,44409 |
| 4 | -0,262616392 | 17 | 0,188865 |
| 5 | 0,179398893 | 18 | 0,21898 |
| 6 | -0,00735706 | 19 | -0,34919 |
| 7 | -0,074570718 | 20 | -0,03768 |
| 8 | -0,033569017 | 21 | 0,674093 |
| 9 | 0,236141895 | 22 | -0,90173 |
| 10 | -0,323321834 | 23 | 0,190798 |
| 11 | 0,185039538 | 24 | 1,350195 |
| 12 | 0,056604813 | 25 | -2,93165 |
| 26 | 1,8 |
Таким образом, получим: 2*N+1=27
Результаты определения порядка фильтров удобно представить в следующем виде:
Таблица 7.
| Фильтр | Полоса пропускания | NTд, с | N | Максимальная точка АЧХ | ||
| ФНЧ1 | 0-0,54 | 0,0042 | 93 | 4,2 | ||
| ПФ1 | 0,54-1 | 0,0043 | 95 | 4,3 | ||
| ПФ2 | 1-2,9 | 0,0162 | 36 | 1,6 | ||
| ПФ3 | 2,9-7 | 0,0009 | 20 | 0,88 | ||
| ПФ4 | 7-11 | 0,0006 | 13 | 0,56 | ||
После ограничения функции и внесения запаздывания можно произвести вычисление коэффициентов фильтра:
a0=k(0)=a2N;
a1=k(T д )=a2N-1;
a2=k(2*T д )=a2N-2;
…
aN=k(N*T д ).
Получив массив коэффициентов, можно записать АФЧХ фильтра с конечным импульсным откликом.
H(Z)=a0+a1*Z^-1+…+a2N+1*Z^-(2N+1), Z=e^jwt
H(jw)=a0+a1*e^-jwt+…+a2N+1*e^-(2N+1)*jwt=a0+a1*Cos(w*Tд)+…+a2N+1*Cos(2N+1)*w*Tд-j*(a1*SinwTд+…+a2N+1*Sin(2N+1)wTд)
Запишем это выражение в более удобной для программирования форме:
H(jw)=Re(w)+jJm(w),
ТогдаАЧХфильтра
/H(jw)/= Re^2(w)+Jm^2(w)

Рис.8. Общая схема DSP-системы
Сигнал, поступающий на аналоговый вход системы предварительно ограничивается по частоте с помощью противопомехового фильтра нижних частот. Затем он передается на АЦП. В выделенный момент дискретизации конвертер прерывает работу процессора и формирует соответствующую выборку.
В DSPвходные данные обрабатываются по программному алгоритму. Когда процессор заканчивает необходимые вычисления, он посылает результат в ЦАП. ЦАП конвертирует выход DSP в желаемую аналоговую форму. Выход конвертора сглаживается восстанавливающим фильтром нижних частот.
Произвольный главный машинный интерфейс служит для связи DSPс внешними системами, передающими и принимающими данные и сигналы управления.
Организация интерфейса между устройствами аналогового
ввода-вывода, кодеками и DSP -процессорами.
Так как большинство приложений цифровой обработки сигналов требует наличия одновременно АЦП и ЦАП, то широкое развитие получили универсальные устройства, интегрирующие функции кодека и портов ввода-вывода на одном кристалле и обеспечивающие простое подключение к стандартным DSP-процессорам. Эти устройства называют аналоговыми оконечными устройствами (далее по тексту-AFE-AnalogFrontEnd ) .