Реферат: Реактивні двигуни

Виконав: студент групи Г-11

Кайда Юрій Володимирович

Хорол 2006

План

1. Визначення реактивного двигуна

2. Принципова схема будови і роботи реактивного двигуна

3. Область застосування реактивного двигуна

4. Переваги і недоліки реактивного двигуна

5. ККД реактивного двигуна і способи його підвищення

Джерела інформації

1. Визначення реактивного двигуна

Сам термін „реактивний” походить від слова „реакція”. Поясню, що ж таке реакція взагалі з фізичної точки зору. Приміром, на столі чи на підлозі лежить предмет (маю на увазі в полі тяжіння). З силою F = mg цей предмет тисне на опору, і тільки тому предмет не рухається у полі тяжіння, що існує реакція опори, рівна за абсолютною величиною вазі предмета, тобто mg, але протилежно напрямлена (дві сили взаємно компенсуються). Це ж саме нам говорить третій закон Ньютона – закон дії і протидії. Правда даний закон – частковий випадок взаємодії тіл і справедливий лише у випадках статичних взаємодій та симетричного зіштовхування цілком однакових куль.

Розглянемо такий приклад. Установимо звичайний електровентилятор на таці невеликої маси, на колесиках також невеликої маси і з невеликим коефіцієнтом тертя в осях, на рівній поверхні. Якщо після ввімкнення вентилятора струмінь повітря буде спрямований „на нас”, то реакція цього струменя буде спрямована „від нас”. У цьому ж напрямку (за реакцією повітряного потоку) вентилятор і покотиться.

Іншим прикладом реактивного двигуна може бути ракета як система двох тіл – оболонки і пального, що знаходиться в ній. Під час запуску ракети пальне згоряє і перетворюється в газ високої температури і високого тиску. Завдяки високому тиску цей газ з великою швидкістю вихоплюється з сопла ракети, внаслідок цього оболонка летить в протилежному напрямку. Саме реакція струменю газу, спрямована протилежно його витіканню і є рушійною силою ракети. Причому, на відміну від вищезгаданої реакції опори, яка виникає в гравітаційних полях, реакція газового струменю має місце також поза межами гравітаційних полів, де з високою ступінню точності систему оболонка – пальне можна вважати замкненою. Як ми побачимо далі, реактивний рух є цікавим і важливим випадком використання закону збереження імпульсу.

2. Принципова схема будови і роботи реактивного двигуна

оболонка

пальне, що знаходиться в оболонці

реактивне сопло

напрямок витікання газів напрямок руху ракети

рис.1

Принципову схему будови і роботи реактивного двигуна показано на рис.1.

Перед стартом ракети її загальний імпульс (оболонки і пального) у системі координат, зв’язаній із Землею, дорівнює нулю, бо вся ракета перебуває в спокої відносно Землі. Внаслідок взаємодії газу й оболонки газ, що викидається, набуває деякого імпульсу. Для спрощення знехтуємо впливом сили тяжіння, тоді оболонку і пальне можна вважати замкненою системою. Загальний імпульс вказаної замкненої системи після запуску також має дорівнювати нулю, тому оболонка через взаємодію з газом набуває імпульсу, рівного за абсолютною величиною, але протилежного йому за напрямком. Ось чому починає рухатися не тільки газ, а й оболонка ракети.

Закон збереження імпульсу дає можливість визначити швидкість ракети (оболонки). Припускаємо, що газ, який утворюється під час згоряння пального, вихоплюється з ракети відразу, а не витікає поступово. Позначимо масу газу, в який перетворюється пальне в ракеті, через mг, а швидкість витікання газу через vг. Масу і швидкість оболонки позначимо через mоб і vоб. Тоді за законом збереження імпульсу

mгvг + mобvоб = 0, звідки 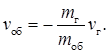(1)

З даної формули видно, що швидкість оболонки ракети тим більша, чим більша швидкість газу, що викидається і чим більше відношення маси пального до маси оболонки.

Більш точно реактивний рух характеризує рівняння Ціолковського, в якому відкинуто припущення про миттєвий викид газу (розглядається рух тіла змінної маси). Для виведення рівняння Ціолковського запишемо диференціальне рівняння руху ракети:

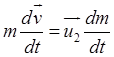(2)

де і m – швидкість і маса ракети у довільний момент часу, u2 – відносна швидкість продуктів згоряння на виході з двигуна (вектор , як відносну швидкість повітря, що поступає до двигуна, опущено, так як вважають ). Вектори та спрямовані в протилежні боки, тому рівність (2) набере вигляду 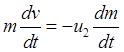(3)

Інтегруючи (3) при u2 = const отримаємо рівняння Ціолковського:

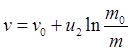(4)

--> ЧИТАТЬ ПОЛНОСТЬЮ <--