Реферат: Решение матричных уравнений Базисный минор Ранг Действия над матрицами
Теорема 2. Матрица ![]() имеет обратную
имеет обратную ![]() только в том случае, если она невырожденная .
только в том случае, если она невырожденная .
Доказательство. Пусть для матрицы ![]() существует обратная
существует обратная ![]() , тогда
, тогда ![]() . Отсюда следует, что
. Отсюда следует, что
![]() ,
,
иначе единицы справа быть не может.
Теорема 3. У каждой невырожденной матрицы существует единственная обратная ![]() .
.
Доказательство. Пусть ![]() имеет две обратные матрицы
имеет две обратные матрицы ![]() и
и ![]() . Тогда
. Тогда
![]() и
и ![]() .
.
Теорема 4. У каждой невырожденной квадратной матрицы существует обратная, равная 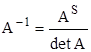 .
.
Докажем эту теорему, вычисляя ![]() . Очевидно, что мы должны получить при этом матрицу
. Очевидно, что мы должны получить при этом матрицу ![]() , элементы которой находятся по формуле
, элементы которой находятся по формуле
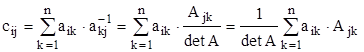 .
.
В полученном выражении, если ![]() , то
, то ![]() . Действительно,
. Действительно, 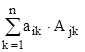 похоже на выражение для вычисления величины определителя. При этом элементы
похоже на выражение для вычисления величины определителя. При этом элементы ![]() -ой строки умножаются на алгебраические дополнения
-ой строки умножаются на алгебраические дополнения ![]() -го столбца. Но так как эти дополнения содержат в себе
-го столбца. Но так как эти дополнения содержат в себе ![]() -ую строку, то получается, что мы вычисляем определитель с двумя одинаковыми строками. Значит, он равен нулю.
-ую строку, то получается, что мы вычисляем определитель с двумя одинаковыми строками. Значит, он равен нулю.
Итак, если ![]() , то
, то ![]() . Если же
. Если же ![]() , то полученное выражение в точности соответствует формуле для вычисления определителя. Значит,
, то полученное выражение в точности соответствует формуле для вычисления определителя. Значит,


![]()
Но ![]() определяет диагональные элементы. Значит, в полученной матрице по главной диагонали стоят единицы, а остальные элементы - нули. Это единичная матрица
определяет диагональные элементы. Значит, в полученной матрице по главной диагонали стоят единицы, а остальные элементы - нули. Это единичная матрица ![]() . Следовательно,
. Следовательно, ![]() и
и 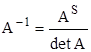 .
.
Отсюда следует правило вычисления обратной матрицы:
1. находим ![]() (он должен быть не равен нулю);
(он должен быть не равен нулю);
2. транспонируем матрицу ![]() ;
;
3. заменяем каждый элемент транспонированной матрицы его алгебраическим дополнением;
4. делим каждый полученный элемент на ![]() .
.
3. Решение матричных уравнений
Понятие обратной матрицы дает возможность решать матричные уравнения. Пусть имеется уравнение вида ![]() , где
, где ![]() ,
, ![]() ,
, ![]() ,
, ![]() - некоторые матрицы, причем
- некоторые матрицы, причем ![]() - неизвестная. Для нахождения
- неизвестная. Для нахождения ![]() , прежде всего, необходимо
, прежде всего, необходимо ![]() перенести вправо:
перенести вправо: ![]() . Затем, пользуясь тем, что
. Затем, пользуясь тем, что ![]() , умножим равенство на
, умножим равенство на ![]() :
:
![]() .
.
При решении подобных уравнений необходимо учитывать, с какой стороны стоит множитель при ![]() . Если уравнение имеет вид
. Если уравнение имеет вид ![]() , то
, то
![]() .
.
Если же уравнение имеет множители при ![]() с обеих сторон
с обеих сторон
(![]() ), то
), то ![]() .
.
4. Базисный минор и ранг матрицы
Введя понятие линейной комбинации строк и столбцов матрицы, как это было сделано у векторов, можно ввести понятие их линейной зависимости и независимости.
Определение 1. Строки ![]() ,
, ![]() ,...,
,..., ![]() называются линейно зависимыми, если существуют числа
называются линейно зависимыми, если существуют числа ![]() , не все равные нулю, такие что справедливо равенство
, не все равные нулю, такие что справедливо равенство ![]() .
.
Здесь 0 - нулевая строка.
Определение 2. Строки ![]() называются линейно независимыми, если их линейная комбинация обращается в ноль лишь при условии, что
называются линейно независимыми, если их линейная комбинация обращается в ноль лишь при условии, что ![]() .
.