Реферат: Решение задач на построение сечений многогранников
Из истории начертательной геометрии
3
Виды проецирования
5
Пересечение многогранников плоскостью (описание метода)
12
Примеры задач
14
Список используемой литературы
Из истории начертательной геометрии.
Еще в глубокой древности человек чертил и рисовал на скалах, камнях, стенах и предметах домашнего обихода изображения вещей, деревьев, животных и людей. Он делал это для удовлетворения своих потребностей, в том числе эстетических. При этом основное требование к таким изображениям заключалось в том, чтобы изображение вызывало правильное зрительное представление о форме изображаемого предмета.
Римский архитектор Витрувий еще в 1 в. до н. э. применял три проекции – план, фасад и профиль. Витрувий рассказывает в своем труде «Десять книг об архитектуре», что еще в V в. до н. э. Агафарх, Демокрит и Анаксагор пользовались элементами перспективы при создании декорации для театра, когда исполнялись «Прикованный Прометей» и другие трагедии великого древнегреческого драматурга Эсхила (525-456 гг. до н. э.).
С ростом практических и технических применений изображений (в строительстве зданий и других гражданских и военных сооружений и т. п.) к ним стали предъявлять и такие требования, чтобы по изображению можно было судить о геометрических свойствах, размерах и взаиморасположении отдельных элементов определенного предмета. О таких требованиях можно судить по многим памятникам древности, уцелевшим до наших дней. Однако строгие геометрические обоснованные правила и методы изображения пространственных фигур (с соблюдением перспективы) стали систематически разрабатывать художники, архитекторы и скульпторы лишь в эпоху Возрождения: Леонардо да Винчи, Дюрер, Рафаэль, Микеланджело, Тициан и др.
Об изображениях, выполненных методами, близкими к аксонометрии, свидетельствуют русские фрески и иконописная живопись XIV-XVI вв. Отсутствием перспективы характеризуются многие русские миниатюры с технической тематикой.
Основы математической теории перспективы были впервые разработаны Ж. Дезаргом в 1630 г. В русских чертежах XVIII в. применяются, кроме перспективных и аксонометрических, также ортогональные проекции. Последние, в частности, использовались выдающимися русскими изобретателями И. И. Ползуновым и И. П. Кулибиным.
Растущие запросы архитектуры, техники, промышленности, военного дела и живописи привели к формированию специальной математической ветви – начертательной геометрии, завершенной французским математиком Г. Монжем. Труд последнего «Начертательная геометрия», возникший из решений ряда вопросов фортификации и опубликованный в 1798 г., лег в основу проекционного черчения, которое широко используется в современной технике и науке. В своей книге Монж разработал метод ортогонального проектирования пространственных фигур на две взаимно перпендикулярные плоскости («метод Монжа»), получая двойное изображение оригинала – на горизонтальной и на вертикальной плоскостях. Это дает возможность решить и обратную задачу: восстановление пространственной фигуры или изучение ее геометрических свойств по заданным (горизонтальному и вертикальному) изображениям, а также решение различных задач, касающихся пространственных фигур, с помощью их плоских изображений.
Недостатком метода Монжа является малая наглядность. Поэтому во многих вопросах, в частности в школе, наиболее употребительным является более наглядный, аксонометрический метод, основанный на параллельной проекции.
Наиболее наглядное изображение пространственных фигур на плоскости дает центральная проекция – перспектива, требующая, однако, дополнительных условий для решения обратной задачи, о которой говорилось выше. Существуют и другие способы изображения пространственных фигур (проекции с числовыми отметками, федоровские проекции и т. д.).
Первая оригинальная русская книга по начертательной геометрии была опубликована в 1821 г. Я. А. Севастьяновым. Разные прикладные вопросы начертательной геометрии разрабатывались академиком И. И. Сомосовым и профессором В. И. Курдюмовым. Значительный научный вклад в развитие начертательной геометрии внес крупный русский кристаллограф и геометр Е.С. Федоров (1853-1919). Своими трудами он способствовал не только развитию теории групп, но и заложению основ многомерной начертательной геометрии. Со второй половины прошлого столетия на развитие начертательной геометрии стала оказывать значительное влияние проективная геометрия. Понятия проективной геометрии для построения начертательной широко использовали А. К. Власов, Н. А. Рынин и другие советские математики.
(«История математики в школе» Г.И.Глейзер)
Виды проецирования
Методом начертательной геометрии является графический метод, основанный на операции проецирования - бинарная конструктивная модель пространства, пространственных форм и отношений, т.е. метод плоскостных (бинарных, двумерных) моделей пространств.
Нам необходимо строить плоскостные модели пространств и по ним уметь решать разнообразные пространственные задачи. Если трёхмерные пространственные формы сформированы на двухмерной плоскости - это чертёж. Чертёж - это определённая совокупность точек и линий на плоскости. Начертательная геометрия занимается построением чертежей пространственных форм и отношений. Какие же двухмерные чертежи могут быть моделями, которые бы отображали свойства пространства, пространственные формы и отношения?
Тут возникает два вопроса:
- Как образовать, как получить такие модели? (Как строить такие чертежи, чтобы они были отображением пространства)
- Что изображать на этой модели (чертеже), чтобы эта модель могла отражать пространственные формы и отношения?
Отвечая на первый вопрос, можно сказать, что каждый чертёж построен по методу проекций. Существует два вида проецирования: центральное и параллельное.
Центральное проецирование.
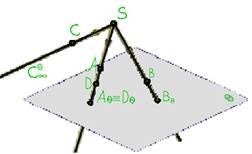
Центральное проецирование - наиболее общий случай получения проекций геометрических фигур. Сущность его состоит в следующем:
|
Рис.1 |
Пусть даны плоскость [SA) |
Плоскость ![]() называют плоскостью проекций, точку S - центром проекции, полученную точку A
называют плоскостью проекций, точку S - центром проекции, полученную точку A![]() - центральной проекцией точки А на плоскость
- центральной проекцией точки А на плоскость ![]() , [SA
, [SA![]() ) - проецирующим лучом.
) - проецирующим лучом.
Аппарат центрального проецирования задан, если задано положение плоскости проекций ![]() и центра проекций S. Если аппарат проецирования задан, то всегда можно определить положение центральной проекции любой точки пространства на плоскости проекций.
и центра проекций S. Если аппарат проецирования задан, то всегда можно определить положение центральной проекции любой точки пространства на плоскости проекций.
Например: Дана точка B. Проведём проецирующий луч [SB) и определим точку встречи его с плоскостью ![]() . Это и есть центральная проекция B
. Это и есть центральная проекция B![]() точки B при заданном аппарате проецирования (
точки B при заданном аппарате проецирования (![]() ,S).
,S).
Если точка С расположена так, что проецирующий луч [SС) ![]()
![]() , то он пересечёт плоскость проекций в несобственной точке С
, то он пересечёт плоскость проекций в несобственной точке С![]() .
.
--> ЧИТАТЬ ПОЛНОСТЬЮ <--