Реферат: Резисторы и конденсаторы в «полупроводниковом» исполнении. Топологические решения и методы расчета
где Т — температура.
Если в интервале температур (T2 —T1 ) изменение сопротивления ( R 2 — R 1 ) связано с изменением температуры линейной зависимостью, то ТКС описывается формулой
![]() (2.5)
(2.5)
Таблица 2.1
Nbg Тип резистора | Номинальные значения сопротивления, Ом | Погрешность, % | Удельное сопротивление, ркв , Ом/кв | ТКС, 1/град |
Эмиттерный слой | 2,5-103 | + 10 | 2-6 | 2*10-3 |
Базовый слой | 150 – 20*103 | + 10 | 50-250 | 2*10-3 |
Коллекторный слой | 250 – 10*103 | + 10 | 200-300 | 5*10-3 |
Сжатые резисторы | (5 – 500)*103 | + 20 | (2-10)*103 | 5*10-3 |
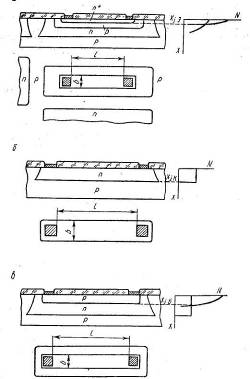

Рисунок 2.1 Структуры резисторов полупроводниковых микросхем: а —на основе эмиттерного слоя; 6 —на основе базового слоя; в —на основе коллекторного слоя; г—сжатый резистор на основе базового слоя; д— сжатый резистор на основе коллекторного слоя.
Полупроводниковые резисторы обладают паразитной распределенной емкостью, что является их недостатком. Паразитная емкость может быть охарактеризована коэффициентом
![]() (2.6)
(2.6)
где Скв — удельная паразитная распределенная емкость квадрата резистивной полоски, пФ/кв; ,ркв — сопротивление квадрата резистивной полоски, кОм/кв; b — ширина резистора, мкм. :
Значения коэффициента Кн для некоторых вариантов резисторов приведены В таблице.
К недостаткам полупроводниковых резисторов относятся также сравнительно высокий ТКС и зависимость номинального сопротивления от величины приложенного к резистору напряжения, которое может модулировать площадь поперечного сечения резистивной полоски вследствие полевого эффекта. Кроме того, в резисторах, изолированных р- n-переходом, может проявляться паразитный транзисторный эффект. Максимально допустимое напряжение зависит от характеристики слоя, образующего резистор, и определяется пробивным напряжением р — л-перехода, отделяющего резистивный слой от остальных областей структуры.
Использование ионной имплантации примесей позволяет получать тонкие резистивные слои с высоким удельным сопротивлением ркв , а также ТКС, слабо изменяющимся в достаточно широком интервале температур. Применяя дополнительную селективную обработку резистивного слоя лучом лазера, можно корректировать сопротивление резистора за счет изменения профиля распределения примесей в данной части слоя.
Достоинствами резисторов, изготовленных нанесением на поверхность кристалла ИМС металлических или поликристаллических кремниевых пленок, являются независимость их сопротивления от величины напряжения, поданного на резистор, а также меньшие паразитные емкости и ТКС по сравнению с диффузионными или имплантированными резисторами. Металлические и поликремниевые резисторы также поддаются корректировке путем пропускания через них электрического тока (плотность тока в импульсе не менее 106 А/см2 ) или обработки лучом лазера. Изменение сопротивления при этом происходит вследствие изменений кристаллической: структуры пленок (размеров зерен, перераспределения примесей и т. п.).
Коэффициент паразитной емкости резисторов Таблица 2.2
| Тип резисторов | Коэффициент К R (пФ/(кОм-мкм2 )) при удельном сопротивлении эпитаксиального коллекторного слоя р | ||
| р=1 Ом-см | р=6 Ом-см | р=10 Ом-см | |
|
Базовый слой Сжатые резисторы на основе: базового слоя коллекторного слоя | 1*10-3 2,7*10-5 8*10-5 | 5*10—4 1,6*10-3 4*10-5 | 4,5*10-4 1,1*10-5 2,8*10-5 |
Расчет диффузионных и имплантированных резисторов заключается в определении их геометрических размеров с учетом профиля распределения примесей в полупроводниковых слоях. Основными условиями, принимаемыми во внимание при расчете, являются обеспечение необходимой мощности рассеяния резистора и заданной погрешности номинального сопротивления. С одной стороны, исходя из условия заданной мощности рассеяния Р и допустимой удельной мощности Ро , можно выразить площадь, занимаемую резистивным слоем, как S = P / P 0 . С другой стороны, площадь определяется геометрическими размерами S = = l / b . Поскольку длина резистивной полоски равна l = bk ф , то площадь может быть выражена соотношением S = b 2 k ф . Таким образом, минимальная ширина резистивной полоски, найденная из условия рассеиваемой мощности, определяется выражением
![]() (2.7)
(2.7)
Максимально допустимая удельная рассеиваемая мощность составляет Ро=8 Вт/мм2 для диффузионных и имплантированных резисторов. Номинальная рассеиваемая мощность полупроводниковых резисторов обычно не превышает 10 мВт.
Требования, предъявляемые к допустимой погрешности номинального значения сопротивления резистора, также ограничивают номинальную ширину резистивной полоски. Если задана допустимая относительная погрешность сопротивления резистора уя — = AR / R , которая должна обеспечиваться в интервале рабочих температур микросхемы в течение всего периода эксплуатации (в том числе без электрической нагрузки), то расчет резистора ведется с учетом ТКС и изменения сопротивления вследствие процессов временного старения.
Относительное отклонение сопротивления вследствие изменения температуры определяется как
![]() (2.8)
(2.8)
Относительное изменение сопротивления из-за процессов старения -улт целесообразно учитывать только для поликремниевых и металлических резисторов, поскольку их пленочная поликристаллическая структура более чувствительна к воздействию окружающей среды, чем монокристаллические слои диффузионных или имплантированных резисторов. Данные о величинах yRc ? являются эмпирическими справочными параметрами.
Кроме того, систематическое отклонение от номинального сопротивления резистора вносится сопротивлениями контактов. Сопротивление контакта зависит от удельного сопротивления материала резистивного слоя и условий растекания тока в приконтактной области: Rконт = ркв k раст , где коэффициент растекания kраст = 0,14 для резистора с топологией, изображенной на рисунке 2.2, а, и Кр аст = 0,65 — на рисунке 2.2, б.

Рисунок 2.2. Топологические конфигурации полупроводниковых резисторов: а— низкоомный резистор; б— высокоомный резистор.
Относительное изменение сопротивления резистора вследствие наличия двух контактов составит
![]() (2.9)
(2.9)
Принимая во внимание указанные систематические отклонения сопротивления резистора от заданного, найдем расчетное значение допустимой относительной погрешности:
![]() (2.10)
(2.10)
Полученное значение ![]() R расч может быть положено в основу дальнейшего расчета резистора с учетом случайных отклонений сопротивления, возникающих в процессе изготовления. Исходя из формулы выразим относительную технологическую погрешность (среднеквадратичное отклонение при. нормальном законе статистического распределения) следующим образом:
R расч может быть положено в основу дальнейшего расчета резистора с учетом случайных отклонений сопротивления, возникающих в процессе изготовления. Исходя из формулы выразим относительную технологическую погрешность (среднеквадратичное отклонение при. нормальном законе статистического распределения) следующим образом:
![]() (2.11)
(2.11)
Где ![]() ,
, ![]() ,
, ![]() - относительные и абсолютные СКО соответствующих величин.
- относительные и абсолютные СКО соответствующих величин.
Полагая, что абсолютные среднеквадратичные отклонения геометрических размеров длины и ширины равны, т. е. ![]() l~
l~![]() b, и учитывая равенство l = bk ф , преобразуем формулу к виду
b, и учитывая равенство l = bk ф , преобразуем формулу к виду
![]() (2.12)
(2.12)
Из последнего соотношения может быть определена минимальная ширина резистивной полоски:
![]() (2.13)
(2.13)
Для типовых технологических процессов изготовления полупроводниковых ИМС можно принимать АЬ = 0,5 мкм и ypkb =0>05.
Полученные в результате расчета по формулам значения ширины резистивной полоски должны быть сопоставлены с минимальной шириной линии, обеспечиваемой принятой технологией, т. е. с разрешающей способностью технологии, бтехн. Принимается максимальное из трех полученных значений
![]() (2.14)
(2.14)
которое окончательно округляется в большую сторону.
Удельное сопротивление квадрата площади резистивиого слоя зависит от толщины слоя и структуры резистора. Резистивный слой может быть ограничен одним (Рисунок 2.1, а — в) или двумя р — n-переходами. Поскольку примесь в полученном диффузией резистивном слое распределена неравномерно, расчет удельного объемного сопротивления материала слоя трудоемок.
Номограммы позволяют найти усредненную удельную объемную проводимость о резистивного слоя в зависимости от поверхностной концентрации акцепторных примесей Ns а , концентрации донорных примесей в исходном материале (эпитаксиальном слое) Nd 0 и отношения текущей координаты х р —n -перехода (если он имеется), ограничивающего резистивный слой сверху, к глубине р — n -перехода Xj , ограничивающего резистивный слой снизу. Например, для резистора, изображенного на рисунке 2.1, а, это отношение x|xj = 0, поскольку резистивный слой начинается непосредственно на поверхности кристалла.