3. Рассчитаем среднегодовые показатели динамики.

3.1. Среднегодовой темп роста :

3.2. Среднегодовой темп прироста :

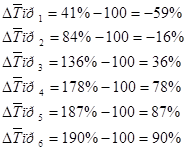3.3. Средний абсолютный прирост :

;

4. Произведем сглаживание ряда методом 3-х летней скользящей средней. Посчитаем по данным таблицы 4 средний уровень реализации за первые 3 года:

(млн.кВт),

затем за 3 года, но начиная не с 1997, а с 1998 года:

(млн.кВт),

затем за 3 года, но начиная не с 1998, а с 1999 года:

(млн.кВт),

затем за 3 года, но начиная с 2000 года:

(млн.кВт),

затем за 3 года, но начиная с 2001 года:

(млн.кВт).

Теперь полученные данные отобразим в таблице 5:

Таблица 5. Расчет скользящей средней

Годы	Мощность ГЭС, млн. кВт	Трехлетняя сумма уровней для скользящего периода, млн.кВт	Трехлетняя скользящая средняя, млн.кВт
1997	22,2	—	—
1998	31,4	94,5	31,5
1999	40,9	124,6	41,53
2000	52,3	154,9	51,63
2001	61,7	177,8	59,27
2002	63,8	189,8	63,27
2003	64,3	—	—

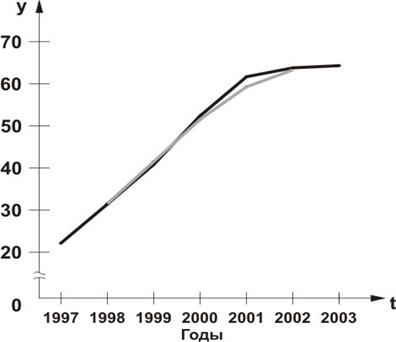
Рисунок 4. Сглаживание ряда динамики мощности ГЭС скользящей средней: линия черным цветом - фактические данные, серым цветом - сглаженные.

5. Выровняем ряд по прямой.

При выравнивании по прямой линии закономерно изменяющиеся уровни динамического ряда рассчитываются как функция времени, выражающаяся уравнением:

Параметры аналитического уравнения выбранной линии находят, используя способ наименьших квадратов . В этом случае предполагается, что сумма квадратов отклонений фактических уровней (y ) от выровненных ( ), т.е. расположенных на искомой линии, должна быть минимальной:

Рассмотрим технику выравнивания ряда динамики по уравнению тренда прямой:

,

где t – условное обозначение времени; a₀ и a₁ – параметры искомой прямой.

Параметры a₀ и a₁ , удовлетворяющие методу наименьших квадратов, находятся путем решения следующей системы нормальных уравнений:

; ;

,

где y - фактические уровни ряда динамики; n – число уровней ряда; t – нумерация фактора времени.

Эта система уравнений значительно упрощается, если значения t подобрать так, чтобы их сумма равнялась нулю. Тогда получается следующая система уравнений:

;