Реферат: Розробка методу формування зони безпечного руху судна

При формуванні безпечної суднової зони судно не можна розглядати у вигляді крапки, площу судна в площині горизонту необхідно враховувати спільно з областю , причому габарити судна в першому наближенні доцільно враховувати таким чином: межа області зміщується на половину довжини судна по напряму діаметральної площини і на половину ширини перпендикулярно їй. Одержану область з урахуванням габаритів судна позначена (рис.1). Якщо приріст до області розглянути у вигляді радіальних приростів поточного радіусу кривизни щодо центру області, то максимальні значення досягаються у напрямі діаметральної площини і рівня L/2, а мінімальні – перпендикулярно діаметральній площині і складають B/2.

Завершальним, третім чинником є урахування динаміки рухомого судна, що обумовлює необхідність додаткового запасу простору для маневру. Цей чинник враховується у вигляді деякої області в просторі істинного, а частіше відносного руху.

Рис 1. Урахування габаритів судна при формуванні безпечної зони

Якщо йдеться про попередження зіткнення суден, то, природно, область задається в просторі відносного руху. У найпростішому випадку область задається в просторі відносного руху кругом з радіусом, рівним гранично допустимій дистанції найкоротшого зближення. Оскільки область задана в просторі істинного руху, то і область необхідно з простору відносного руху відобразити в простір істинного руху, і одержану область об'єднати з областю .

Операція перетворення області відносного руху у відповідну область істинного руху передбачає відображення точок границі області в простір істинного руху.

Для безпечної зони судна необхідно здійснити сумісне урахування областей і , тобто . Аналіз можливих альтернатив показав, що доцільним є спосіб складання полярних координат границі області , завданої щодо обсервованого місця судна, з полярними координатами області , одержаним щодо того ж початку координат, як показано на рис. 2.

Для пошуку двовимірної області Z1 використовувався розподіл Гауса, який відноситься до стійких розподілів, а його двовимірна щільність для випадку залежних похибок вимірювань має вигляд:

,

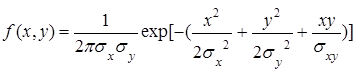де і - середні квадратичні відхилення векторіальної похибки відповідно по осях x і у , а , причому - другий змішаний момент. Якщо похибки вимірювань навігаційних параметрів залежні, то за допомогою методу обертань з коваріаційної матриці можна виключити недіагональний елемент, тобто другий змішаний момент . При цьому змінюються значення дисперсій і , які характеризують діагональну коваріаційну матрицю, яка позначена , а нові значення дисперсій - і , тобто:

Рис 2. Об’єднання областей і в безпечну зону судна

.

Вирази для і приймають вигляд:

;

.

Після вказаних перетворень вираз двовимірної щільності приймає наступний вигляд:

,

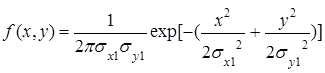причому півосі еліпса є функціями дисперсій і , а також вірогідність попадання істинного місця судна в заданий еліпс.

Якщо півосі еліпса позначити через а (велика) і b (менша), то задачу побудови області формулюється таким чином: знайти півосі еліпса а і b , зберігаючи незмінним його стиснення, при яких виконується рівність:

=.

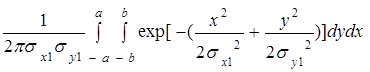Дане рівняння рішається таким чином. Спочатку максимальне значення h щільності розподілу вірогідностей знаходиться з виразу:

.

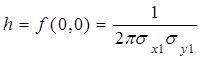Область двовимірної щільності, яка відсікається площиною 1-1, як показано на рис. 3, рівна по величині гранично допустимій вірогідності , є сумою складових, що мають форму еліпса, товщиною  h . Якщо кожну складову позначити , то: .

Рис. 3. Пошук параметрів стохастичної області Z1

Починаючи з першої, верхньої, еліптичної складової з мінімальними півосями, додаються подальші складові, причому ведеться контроль за сумою складових. Коли сума складових найближче рівна значенню, то півосі останньої складової є шуканими параметрами стохастичної області .

При цьому визначається кут , під яким еліпс орієнтований відносно опорної системи координат з допомогою виразу:

.

Урахування динаміки рухомого судна при формуванні безпечної суднової зони вимагає додаткового запасу простору для маневру, яке, як правило, є деякою областю, причому її доцільно задавати в просторі відносного руху, з тим, щоб уникнути можливих зіткнень зі стрічними суднами. Для нерухомих об'єктів, зона буде задана в просторі істинного руху. Саме в просторі істинного руху задані інші складові безпечної суднової зони (за габарити судна, за точність контролю його місця), тому область, що враховує динаміку судна, необхідно відобразити з простору відносного в простір істинного руху. Таке відображення можливе в три етапи: спочатку необхідно завдати аналітичний вираз для області в просторі відносного руху, потім записати цей вираз в полярних координатах відносно судна або цілі і, нарешті, виконати перетворення кожної точки границі безпечної суднової зони з простору відносного руху в простір істинного.

У простому випадку, як вже наголошувалося, область задається в просторі відносного руху кругом радіусу R , рівним гранично допустимій дистанції найкоротшого зближення.У роботі показано, що рівняння кола в полярних координатах і відносно центру, розташованого по пеленгу і дистанції від судна, має наступний аналітичний вираз:

, ,

де - вільний параметр, що змінюється від нуля до 2р.

Якщо область задається еліпсом з великою b і малої а півосями, його також можна задати в параметричному вигляді, аналогічно попередньому випадку, тільки необхідно ввести змінний радіус R :

.

В цьому випадку прямокутні координати еліпсу розраховуються слідуючими формулами:

і .

Потім за допомогою стандартної процедури необхідно виконати поворот системи координат на величину курсу судна і врахувати зміщене положення центру еліпса щодо центру судна. Перетворення в полярні координати і здійснюється згідно вищенаведеним виразам.

Якщо безпечна зона задається лише шириною b і завдовжки по носу та кормі судна значеннями і , то її доцільно використовувати у вигляді прямокутника із заданими параметрами (рис. 4), який визначається чотирма кутовими крапками 1, 2, 3 і 4, завданими відносно центру судна.

З урахуванням курсу судна K і положення його центру, в опорній системі координат, координати кутових крапок 1, 2, 3 і 4 в цій же координатній системі визначаються наступними виразами:

=+, =+,