Реферат: Сетевые модели планирования и управления
Где нормированное отклонение случайной величины: z = (Т - tKp )/S Kp;
SKp — среднее квадратическое отклонение, вычисляемое как корень квадратный из дисперсии продолжительности критического пути.
Соответствие между z и симметричным интегралом вероятностей приведено в табл. 2. Более точно соответствие между этими величинами (когда z вычисляется более чем с одним знаком в дробной части) можно найти в специальной статистической литературе.
При достаточно большой полученной величине вероятности (более 0,8) можно с высокой степенью уверенности предполагать своевременность выполнения всего комплекса работ.
Для решения второй задачи используется формула:
Т = t ож (Lkp )+ z *S kp
Таблица 2. Фрагмент таблицы стандартного нормального распределения
| z | Фz | z | Фz |
| 0,1 | 0,0797 | 1,5 | 0,8664 |
| 0,2 | 0,1585 | 1,6 | 0,8904 |
| 0,3 | 0,2358 | 1,7 | 0,9104 |
| 0,4 | 0,3108 | 1,8 | 0,9281 |
| 0,5 | 0,3829 | 1,9 | 0,9545 |
| 0,6 | 0,4515 | 2,0 | 0,9643 |
| 0,7 | 0,5161 | 2,1 | 0,9722 |
| 0,8 | 0,5763 | 2,2 | 0,9786 |
| 0,9 | 0,6319 | 2,3 | 0,9836 |
| 1,0 | 0,6827 | 2,4 | 0,9876 |
| 1,1 | 0,7287 | 2,5 | 0,9907 |
| 1,2 | 0,7699 | 2,6 | 0,9931 |
| 1,3 | 0,8064 | 2,7 | 0,9949 |
| 1,4 | 0,8385 | 2,8 | 0,9963 |
Кроме описанного способа расчета сетей с детерминированной структурой и вероятностными оценками продолжительности выполнения работ, используется метод статистических испытаний (метод Монте-Карло). В соответствии с ним на вычислительной технике многократно моделируется продолжительность выполнения работ и рассчитывается на основе этого основные характеристики сетевой модели. Большой объем испытаний позволяет более точно выявить закономерность моделируемой сети.
Вторая глава: Построение сетевой модели
Структура сетевой модели и оценки продолжительности работ (в сутках) заданы в табл. 3. Требуется:
а) получить все характеристики СМ;
б) оценить вероятность выполнения всего комплекса работ за 35 дней, за 30 дней;
в) оценить максимально возможный срок выполнения всего комплекса работ с надежностью 95% (т. е. р = 0,95).
Три первые графы табл. 3. содержат исходные данные, а две последние графы — результаты расчетов по формулам Так, например,
t ож (i,j)=(3tmin (i,j) + 2t max (i,j)) : 5
t ож (1,2)=(3*5 +2*7,5):5 =6
t ож (2,3)=(3*4 +2*6,5):5 =5
S2 ( i,j) = (t max (i,j) – t min (i,j) 2 :5 2 =
= 0.04 ( t max (i,j) – t min (i,j)2
S2 ( 1,2) = (7,5 - 5) 2 :25 =0,25
S2 (2 ,3) = (6,5 - 4) 2 :25 =0,25
| Работа | Продолжительность | Ожидаемая | Дисперсия | |
| ( i,j) | tmin (i,j) | t max (i,j) | Продолжительность t ож (i,j) | S2 ( i,j) |
| (1.2) | 5 | 7.5 | 5 | 0.25 |
| (2.3) | 4 | 6.5 | 5 | 0.25 |
| (2.4) | 3 | 6 | 3 | 1.00 |
| (2.5) | 1 | 5.5 | 4 | 0.25 |
| (3.7) | 0.5 | 3.5 | 1 | 0.36 |
| (4.5) | 5 | 7.5 | 6 | 0.25 |
| (4.6) | 3 | 5.5 | 4 | 0.25 |
| (4.9) | 5 | 10 | 7 | 1.00 |
| (5.8) | 2 | 4.5 | 3 | 0.25 |
| (5.10) | 7 | 12 | 9 | 1.00 |
| (6.9) | 0 | 0 | 0 | 0.00 |
| (6.11) | 3 | 8 | 5 | 1.00 |
| (7.10) | 4 | 9 | 6 | 1.00 |
| (8.10) | 2 | 7 | 4 | 1.00 |
| (9.10) | 1 | 6 | 3 | 1.00 |
| (10.11) | 8 | 10.5 | 9 | 0.25 |
Получим сетевую модель аналогичную рассматриваемой во второй главе:
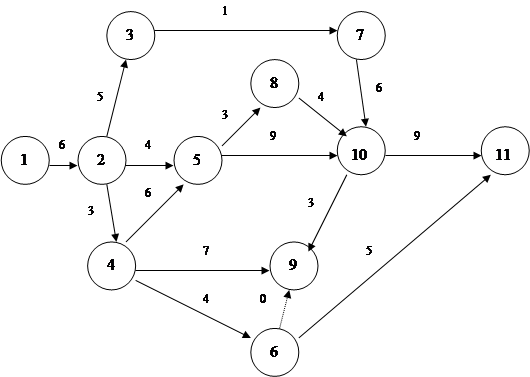 |
Таким образом ход расчета характеристик модели остается аналогичен рассмотренному во второй главе. Напомним, что критическим является путь: L кр = (1,2,4,5,10,11), а его продолжительность равна t кр = t ож = 33 дня.
Дисперсия критического пути составляет:
S2 Kp = S2 (l,2) + S2 (2,4) + S2 (4,5) + S2 (5,10) + S2 (10,M) =
= 0,25 + 1,00 + 0,25 + 1,00 + 0,25 = 2,75.
Для использования формулы показателя дисперсии необходимо иметь среднее квадратическое отклонение, вычисляемое путем извлечения из значения дисперсии квадратного корня, т. е. SKp = 1,66 . Тогда имеем:
Р( t кр <35) = 0,5 + 0,5 Ф{(35 - 33)1,66} =
= 0.5 + 0.5 Ф(1,2)=0,5+0,5*0,77=0,885
Р( t кр <30) = 0,5 + 0,5 Ф{(30 - 33)/1,66} = 0,5 - 0,5Ф(1,8) =
= 0,5 - 0,5 • 0,95 = 0,035.
Таким образом, вероятность того, что весь комплекс работ будет выполнен не более чем за 35 дней, составляет 88,5%, в то время как вероятность его выполнения за 30 дней — всего 3,5% .
Для решения второй (по существу обратной) задачи прежде всего в табл.2 найдем значение аргумента z, которое соответствует заданной вероятности 95% . В графе Ф(z) наиболее близкое значение (0,9545 • 100%) к ней соответствует г = 1,9. В этой связи в формуле (3.61) будем использовать именно это (не совсем точное) значение. Тогда получим:
Т = t ож (L кр ) + z-SKp = 33 + 1,9*1,66 = 36,2 дн.
Следовательно, максимальный срок выполнения всего комплекса работ при заданном уровне вероятности р = 95% составляет 36,2 дня.
Составим словесно-формульное описание алгоритма