Реферат: Сфера S8319

СФЕРА

СОДЕРЖАНИЕ

ВВЕДЕНИЕ................................................................................ 2

МНОЖЕСТВО И РАССТОЯНИЕ В НЁМ..................... 3

ОТКРЫТЫЕ И ЗАМКНУТЫЕ МНОЖЕСТВА В ......... 4

СФЕРА .................................................................................. 5

НЕКОТОРЫЕ СВОЙСТВА СФЕРЫ ............................... 5

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ............. 7

ВВЕДЕНИЕ

Многие величины, представляющие интерес, зависят не от одного, а от очень многих факторов, и если сама величина и каждый из определяющих его факторов могут быть охарактеризованы некоторым числом, то указанная зависимость сводится к тому, что упорядоченному набору чисел, каждое из которых описывает состояние соответствующего фактора, становится в соответствие значение исследуемой величины, которое она приобретает при этом состоянии определяющих величину факторов.

Например, площадь прямоугольника есть произведение длин его сторон; объём данного количества газа вычисляется по формуле

,

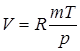где – постоянная, – масса, – абсолютная температура и – давление газа. Таким образом, значение зависит от переменной упорядоченной тройки чисел или, как говорят есть функция трёх переменных .

Мы ставим себе целью научиться исследовать функции многих переменных так же, как мы научились исследовать функции одного переменного.

Как и в случае функции одного переменного, изучение функции многих числовых переменных начинается с описания их области определения.

МНОЖЕСТВО И РАССТОЯНИЕ В НЁМ.

Условимся через обозначать множество всех упорядоченных наборов , состоящих из действительных чисел .

Каждый такой набор будем обозначать одной буквой и в соответствии с удобной геометрической терминологии называть точкой множества .

Число в наборе называют -й координатой точки .

Геометрические аналогии можно продолжить и ввести на множестве расстояние между точками , по формуле

(1)

Функция

,

определяемая формулой (1), очевидно, обладает следующими свойствами:

a) ;

b) ;

c) ;

d) .

Последнее неравенство (называемое опять-таки по геометрической аналогии неравенством треугольника) есть частный случай неравенства Минковского.

Функцию, определённую на парах точек некоторого множества и обладающую свойствами a), b), c), d), называют метрикой или расстоянием в .

Множество вместе с фиксированной в нём метрикой называют метрическим пространством.

Таким образом, мы превратили в метрическое пространство, наделив метрикой, заданной соотношением (1).

Из соотношения (1) следует, что при

(2)

--> ЧИТАТЬ ПОЛНОСТЬЮ <--