1. Шифрування з секретним ключем

Алгоритм RSA є алгоритмом асиметричної криптографії. Він був запропонований трьома дослідниками-математиками Рональдом Ривестом (R. Rivest) , Ади Шамиром (A. Shamir) і Леонардом Адльманом (L. Adleman) в 1977-78 роках.

Першим етапом будь-якого асиметричного алгоритму є створення пари ключів: відкритого і закритого та поширення відкритого ключа "по усьому світу". Для алгоритму RSA етап створення ключів складається з наступних операцій:

1. Вибираються два простих числа p та q

2. Обчислюється їх добуток n=(p*q)

3. Вибирається довільне число e (e<n), таке, що НОД(e,(p-1)(q-1))=1, тобто e повинне бути взаємно простим із числом (p-1)(q-1).

4. Методом Євкліда в цілих числах знаходиться рішення рівняння e*d+(p-1)(q-1)*y=1. Тут невідомими є змінні d і y - метод Евкліда саме і знаходить безліч пар (d,y), кожна з яких є рішенням рівняння в цілих числах.

5. Два числа (e,n) - публікуються як відкритий ключ.

6. Число d зберігається в найсуворішому секреті - це і є закритий ключ, що дозволить читати всі послання, зашифровані за допомогою пари чисел (e,n).

Як же виробляється шифрування за допомогою цих чисел:

1. Відправник розбиває своє повідомлення на блоки, рівні k=[log₂ (n)] біт, де квадратні дужки позначають узяття цілої частини від дробового числа.

2. Подібний блок може бути інтерпретований як число з діапазону (0;2^k -1). Для кожного такого числа (назвемо його m_i ) обчислюється c_i =((m_i )^e )mod n. Блоки c_i і є зашифроване повідомлення Їх можна спокійно передавати по відкритому каналу, оскільки операція зведення в ступінь по модулі простого числа, є необоротним математичним завданням. Зворотна їй операція – "логарифмування в кінцевому полі" є на кілька порядків більше складним завданням. Тобто навіть, якщо зловмисник знає числа e і n, те по c_i прочитати вихідні повідомлення m_i він не може ніяк, крім як повним перебором m_i .

А от на прийомній стороні процес дешифрування все-таки можливий, і допоможе нам у цьому збережене в секреті число d. Досить давно була доведена теорема Ейлера, окремий випадок якої затверджує, що якщо число n представимо у вигляді двох простих чисел p і q, то для будь-якого x має місце рівність (x^(p-1)(q-1) )mod n = 1. Для дешифрування RSA-повідомлень скористаємося цією формулою. Зведемо обидві її частини в ступінь (-y): (x^{(-y)(p-1)(q-1)} )mod n = 1^(-y) = 1. Тепер помножимо обидві її частини на x: (x^{(-y)(p-1)(q-1)+1} )mod n = 1*x = x.

А тепер згадаємо як ми створювали відкритий і закритий ключі. Ми підбирали за допомогою алгоритму Евкліда d таке, що e*d+(p-1)(q-1)*y=1, тобто e*d=(-y)(p-1)(q-1)+1. А отже в останній рівності попереднього абзацу ми можемо замінити показник ступеня на число (e*d). Одержуємо (x^e*d )mod n = x. Тобто для того щоб прочитати повідомлення c_i =((m_i )^e )mod n досить звести його в ступінь d по модулі m: ((c_i )^d )mod n = ((m_i )^e*d )mod n = m_i .

Операції зведення в ступінь більших чисел досить трудомісткі для сучасних процесорів, навіть якщо вони виробляються по оптимізованим за часом алгоритмам. Тому звичайно весь текст повідомлення кодується звичайним блоковим шифром (набагато більше швидким), але з використанням ключа сеансу, а от сам ключ сеансу шифрується саме асиметричним алгоритмом за допомогою відкритого ключа одержувача і міститься в початку файлу.

2. Характеристики стандартних алгоритмів шифрування з секретним ключем

2.1 Симетричне шифрування

Свою історію алгоритми симетричного шифрування ведуть зі стародавності: саме цим способом приховання інформації користувався римський імператор Гай Юлій Цезар в I столітті до н.е., а винайдений їм алгоритм відомий як "криптосистема Цезаря".

У наш час найбільш відомий алгоритм симетричного шифрування DES (Data Encryption Standard), розроблений в 1977 р. Донедавна він був "стандартом США", оскільки уряд цієї країни рекомендував застосовувати його для реалізації різних систем шифрування даних. Незважаючи на те, що DES планувалося використати не більше 10-15 років, його замінили тільки в 1997 р.

Основна причина заміни стандарту шифрування - його відносно слабка криптостойкість, причина якої в тім, що довжина ключа DES становить усього 56 значущий біт. Відомо, що будь-який криптостійкий алгоритм можна зламати, перебравши усі можливі варіанти ключів шифрування (так званий метод грубої сили - brute force attack). Легко підрахувати, що кластер з 1 млн. процесорів, кожний з яких обчислює 1 млн. ключів у секунду, перевірить 256 варіантів ключів DES майже за 20 ч. А оскільки по нинішніх мірках такі обчислювальні потужності цілком реальні, ясно, що 56-бітовий ключ занадто короткий і алгоритм DES необхідно замінити на більш ефективний.

Сьогодні усе ширше використовуються два сучасних крипостійких алгоритми шифрування: вітчизняний стандарт ГОСТ 28147-89 і новий криптостандарт США - AES (Advanced Encryption Standard).

2.2 Стандарт ГОСТ 28147-89

Алгоритм, обумовлений ГОСТ 28147-89 (рис. 1), має довжину ключа шифрування 256 біт. Він шифрує інформацію блоками по 64 біт (такі алгоритми називаються блоковими), які потім розбиваються на два субблоки по 32 біт (N1 і N2). Субблок N1 обробляється певним чином, після чого його значення складається зі значенням субблока N2 (додавання виконується по модулю 2, тобто застосовується логічна операція XOR - "виключне або"), а потім субблоки міняються місцями. Дане перетворення виконується певне число разів ("раундів"): 16 або 32 залежно від режиму роботи алгоритму. У кожному раунді виконуються дві операції.

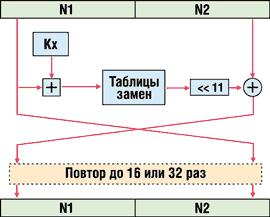
Рисунок 1 – Схема алгоритму ГОСТ 28147-89

Перша - накладення ключа. Вміст субблоку N1 складається по модулю 2 з 32-бітною частиною ключа Kx. Повний ключ шифрування представляється у вигляді конкатенації 32-біт підключів: K0, K1, K2, K3, K4, K5, K6, K7. У процесі шифрування використається один із цих підключів - залежно від номера раунду і режиму роботи алгоритму.

Друга операція - таблична заміна. Після накладення ключа субблок N1 розбивається на 8 частин по 4 біт, значення кожної з яких заміняється відповідно до таблиці заміни для даної частини субблока. Потім виконується побітовий циклічний зсув субблока вліво на 11 біт.

Табличні заміни часто використаються в сучасних алгоритмах шифрування, тому варто пояснити, як організується подібна операція. У таблицю записуються вихідні значення блоків. Блок даних певної розмірності (у нашому випадку - 4-біта) має своє числове подання, що визначає номер вихідного значення. Наприклад, якщо S-box має вигляд 4, 11, 2, 14, 15, 0, 8, 13, 3, 12, 9, 7, 5, 10, 6, 1 і на вхід прийшов 4-біта блок "0100" (значення 4), то, відповідно до таблиці, вихідне значення буде дорівнює 15, тобто "1111" (0 а 4, 1 а 11, 2 а 2...).

Алгоритм, обумовлений ГОСТ 28147-89, передбачає чотири режими роботи: простої заміни, гамування, гамування зі зворотним зв'язком і генерації імітоприставок. У них використається те саме описане вище перетворення але, оскільки призначення режимів по-різному, здійснюється це перетворення в кожному з них по-різному.

У режимі простої заміни для шифрування кожного 64-бітног блоку інформації виконуються 32 описаних вище раунда. При цьому 32-бітні підключи використовуються в наступній послідовності:

K0, K1, K2, K3, K4, K5, K6, K7, K0, K1 і т.д. - у раундах з 1-го по 24-й;

--> ЧИТАТЬ ПОЛНОСТЬЮ <--