Реферат: Синтез оптимальных уравнений
Г л а в а I
ВВЕДЕНИЕ
Управляемые объекты прочно вошли в нашу повседневную жизнь и стали обиходными, обыденными явлениями. Мы видим их буквально на каждом шагу: автомобиль, самолёт, всевозможные электроприборы, снабжённые регуляторами (например, электрохолодильник), и т. п. Общим во всех этих случаях является то, что мы можем «управлять» объектом, можем в той или иной степени влиять на его поведение.
Обычно переход управляемого объекта из одного состояния в другое может быть осуществлён многими различными способами. Поэтому возникает вопрос о выборе такого пути, который с некоторой (но вполне определённой) точки зрения окажется наиболее выгодным. Это и есть (несколько расплывчато сформулированная) задача об оптимальном управлении.
§ 1. Задача об оптимальном быстродействии
1. 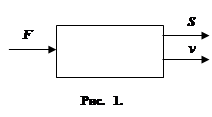 Понятие об управляемых объектах. Рассмотрим прямолинейное движение автомобиля. В каждый момент времени состояние автомобиля можно характеризовать двумя числами: пройденным расстоянием s и скоростью движения v. Эти две величины меняются с течением времени, но не самопроизвольно, а сообразно воле водителя, который может по своему желанию управлять работой двигателя, увеличивая или уменьшая развиваемую этим двигателем силу F. Таким образом, мы имеем три связанных между собой параметра: s ,v ,F ,показанных на схеме (рис. 1). Величины s ,v ,характеризующие состояние автомобиля, называют его фазовыми координатами ,а величину F – управляющим параметром .
Понятие об управляемых объектах. Рассмотрим прямолинейное движение автомобиля. В каждый момент времени состояние автомобиля можно характеризовать двумя числами: пройденным расстоянием s и скоростью движения v. Эти две величины меняются с течением времени, но не самопроизвольно, а сообразно воле водителя, который может по своему желанию управлять работой двигателя, увеличивая или уменьшая развиваемую этим двигателем силу F. Таким образом, мы имеем три связанных между собой параметра: s ,v ,F ,показанных на схеме (рис. 1). Величины s ,v ,характеризующие состояние автомобиля, называют его фазовыми координатами ,а величину F – управляющим параметром .
Если мы будем рассматривать движение автомобиля по плоскости (а не по прямой), то фазовых координат будет четыре (две «географические» координаты и две компоненты скорости), а управляющих параметров – два (например, сила тяги двигателя и угол поворота руля). У летящего самолёта можно рассматривать шесть фазовых координат (три пространственные координаты и три компоненты скорости) и несколько управляющих параметров (тяга двигателя, величины, характеризующие положение рулей высоты и направления, элеронов).
 Разумеется, в проводимом ниже математическом исследовании мы будем иметь дело не с самими реальными объектами, а с некоторой математической моделью. Сказанное выше делает естественным следующее математическое описание управляемого объекта. Состояние объекта задаётся (в каждый момент времени) n числами x 1 , x 2 ,…, xn , которые называются фазовыми координатами объекта. Движение объекта заключается с математической точки зрения в том, что его состояние с течением времени изменяется, т. е. x 1 , x 2 ,…, xn являются переменными величинами (функциями времени). Движение объекта происходит не самопроизвольно. Им можно управлять; для этого объект снабжён «рулями», положение которых характеризуется (в каждый момент времени) r числами u 1 , u 2 ,…, ur ; эти числа называются управляющими параметрами . Рулями можно «манипулировать», т. е. по своему желанию менять (конечно, в допустимых пределах) управляющие параметры u 1 , u 2 ,…, ur . Иначе говоря, мы можем по желанию выбрать функции u 1 ( t), u 2 ( t),…, ur ( t), описывающие изменение управляющих параметров с течением времени. Мы будем предполагать (как это обычно и бывает), что, зная фазовое состояние объекта в начальный момент времени и выбрав управляющие функции u 1 ( t), u 2 ( t),…, ur ( t) (для t> t 0 ), мы можем точно и однозначно рассчитать поведение объекта для всех t> t0 ,т. е. можем найти функции x 1 ( t), x 2 ( t),…, xn ( t), характеризующие изменение фазовых координат с течением времени. Таким образом, изменение фазовых координат x 1 , x 2 ,…, xn уже не зависит непосредственно от нашего желания, но на движение объекта мы всё же можем в той или иной мере воздействовать, выбирая по своему желанию управляющие функции u 1 ( t), u 2 ( t),…, ur ( t) .
Разумеется, в проводимом ниже математическом исследовании мы будем иметь дело не с самими реальными объектами, а с некоторой математической моделью. Сказанное выше делает естественным следующее математическое описание управляемого объекта. Состояние объекта задаётся (в каждый момент времени) n числами x 1 , x 2 ,…, xn , которые называются фазовыми координатами объекта. Движение объекта заключается с математической точки зрения в том, что его состояние с течением времени изменяется, т. е. x 1 , x 2 ,…, xn являются переменными величинами (функциями времени). Движение объекта происходит не самопроизвольно. Им можно управлять; для этого объект снабжён «рулями», положение которых характеризуется (в каждый момент времени) r числами u 1 , u 2 ,…, ur ; эти числа называются управляющими параметрами . Рулями можно «манипулировать», т. е. по своему желанию менять (конечно, в допустимых пределах) управляющие параметры u 1 , u 2 ,…, ur . Иначе говоря, мы можем по желанию выбрать функции u 1 ( t), u 2 ( t),…, ur ( t), описывающие изменение управляющих параметров с течением времени. Мы будем предполагать (как это обычно и бывает), что, зная фазовое состояние объекта в начальный момент времени и выбрав управляющие функции u 1 ( t), u 2 ( t),…, ur ( t) (для t> t 0 ), мы можем точно и однозначно рассчитать поведение объекта для всех t> t0 ,т. е. можем найти функции x 1 ( t), x 2 ( t),…, xn ( t), характеризующие изменение фазовых координат с течением времени. Таким образом, изменение фазовых координат x 1 , x 2 ,…, xn уже не зависит непосредственно от нашего желания, но на движение объекта мы всё же можем в той или иной мере воздействовать, выбирая по своему желанию управляющие функции u 1 ( t), u 2 ( t),…, ur ( t) .
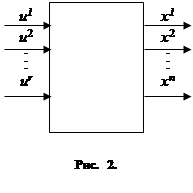
Управляемый объект, о котором только что шла речь, в теории автоматического управления принято изображать так, как это показано на рис. 2. Величины u 1 , u 2 ,…, ur (управляющие параметры) часто называют также «входными переменными», а величины x 1 , x 2 ,…, xn (фазовые координаты) – «выходными переменными». Говорят ещё, что «на вход» объекта поданы величины u 1 , u 2 ,…, ur , а «на выходе» мы получаем величины x 1 , x 2 ,…, xn . Разумеется, на рис. 2 показано лишь условное обозначение управляемого объекта и никак не отражено его «внутреннее устройство», знание которого необходимо, чтобы выяснить, каким образом, зная управляющие функции u 1 ( t), u 2 ( t),…, ur ( t) , можно вычислить изменение фазовых координат x 1 ( t), x 2 ( t),…, xn ( t) .
Величины u 1 , u 2 ,…, ur удобно считать координатами некоторого вектора u= (u 1 , u 2 ,…, ur ), также называемого управляющим параметром (векторным). Точно так же величины x 1 , x 2 ,…, xn удобно рассматривать как координаты некоторого вектора (или точки) x= (x 1 , x 2 ,…, xn ) в n – мерном пространстве с координатами x 1 , x 2 ,…, xn . Эту точку называют фазовым состоянием объекта, а n – мерное пространство, в котором в виде точек изображаются фазовые состояния, называется фазовым пространством рассматриваемого объекта. Если объект таков, что его фазовое состояние характеризуется только двумя фазовыми координатами x 1 , x 2 (см. рис. 1), то мы будем говорить о фазовой плоскости . В этом случае фазовые состояния объекта изображаются особенно наглядно.
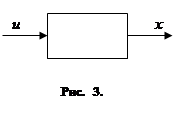 Итак, в векторных обозначениях рассматриваемый управляемый объект можно изобразить так, как показано на рис. 3. Входящая величина u= (u 1 , u 2 ,…, ur ) представляет собой управляющий параметр, а выходная величина x= (x 1 , x 2 ,…, xn ) представляет собой точку фазового пространства (или, иначе, фазовое состояние объекта).
Итак, в векторных обозначениях рассматриваемый управляемый объект можно изобразить так, как показано на рис. 3. Входящая величина u= (u 1 , u 2 ,…, ur ) представляет собой управляющий параметр, а выходная величина x= (x 1 , x 2 ,…, xn ) представляет собой точку фазового пространства (или, иначе, фазовое состояние объекта).
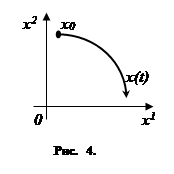 Как сказано выше, чтобы полностью задать движение объекта, надо задать его фазовое состояние x0 = (x 0 1 , x 0 2 ,…, x 0 n ) в начальный момент времени t0 и выбрать управляющие функции u 1 ( t), u 2 ( t),…, ur ( t) (для t >t 0 ), т. е. выбрать векторную функцию u( t)= u 1 ( t), u 2 ( t),…, ur ( t) ). Эту функцию u( t) мы будем называть управлением . Задание начального фазового состояния x0 и управления u( t) однозначно определяет дальнейшее движение объекта. Это движение заключается в том, что фазовая точка x (t)= (x 1 ( t), x 2 ( t),…, xn ( t) ), изображающая состояние объекта, с течением времени перемещается, описывая в фазовом пространстве некоторую линию, называемую фазовой траекторией рассматриваемого движение объекта (случай n= 2 изображён на рис. 4). Очевидно, что эта линия исходит из точки x 0 , поскольку x (t 0 )=x 0 .
Как сказано выше, чтобы полностью задать движение объекта, надо задать его фазовое состояние x0 = (x 0 1 , x 0 2 ,…, x 0 n ) в начальный момент времени t0 и выбрать управляющие функции u 1 ( t), u 2 ( t),…, ur ( t) (для t >t 0 ), т. е. выбрать векторную функцию u( t)= u 1 ( t), u 2 ( t),…, ur ( t) ). Эту функцию u( t) мы будем называть управлением . Задание начального фазового состояния x0 и управления u( t) однозначно определяет дальнейшее движение объекта. Это движение заключается в том, что фазовая точка x (t)= (x 1 ( t), x 2 ( t),…, xn ( t) ), изображающая состояние объекта, с течением времени перемещается, описывая в фазовом пространстве некоторую линию, называемую фазовой траекторией рассматриваемого движение объекта (случай n= 2 изображён на рис. 4). Очевидно, что эта линия исходит из точки x 0 , поскольку x (t 0 )=x 0 .
Пару векторных функций (u( t), x( t) ), т. е. управление u( t) и соответствующую фазовую траекторию x( t) , мы будем называть в дальнейшем процессом управления или просто процессом .
 Итак, резюмируем. Состояние управляемого объекта в каждый момент времени характеризуется фазовой точкой x= (x 1 , x 2 ,…, xn ). На движение объекта можно воздействовать при помощи управляющего параметра u= (u 1 , u 2 ,…, ur ). Изменение величин u, x с течением времени мы называем процессом ; процесс (u( t), x( t) ) составляется из управления u( t) и фазовой траектории x( t) . Процесс полностью определяется, если задано управление u( t) (при t >t 0 ) и начальное фазовое состояние x 0 = x( t 0 ) .
Итак, резюмируем. Состояние управляемого объекта в каждый момент времени характеризуется фазовой точкой x= (x 1 , x 2 ,…, xn ). На движение объекта можно воздействовать при помощи управляющего параметра u= (u 1 , u 2 ,…, ur ). Изменение величин u, x с течением времени мы называем процессом ; процесс (u( t), x( t) ) составляется из управления u( t) и фазовой траектории x( t) . Процесс полностью определяется, если задано управление u( t) (при t >t 0 ) и начальное фазовое состояние x 0 = x( t 0 ) .
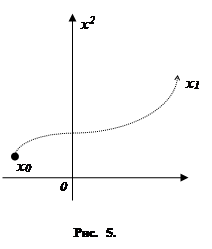
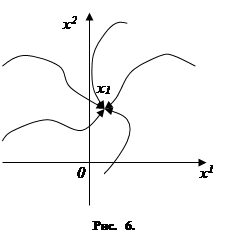
2. Задача управления. Часто встречается следующая задача, связанная с управляемыми объектами. В начальный момент времени t 0 объект находится в фазовом состоянии x 0 ; требуется выбрать такое управление u( t) , которое переведёт объект в заранее заданное конечное фазовое состояние x 1 (отличное от x 0 ; рис. 5). При этом нередко бывает, что начальное состояние x 0 заранее не известно. Рассмотрим один из наиболее типичных примеров. Объект должен устойчиво работать в некотором режиме (т. е. находиться в некотором фазовом состоянии x 1 ). В результате тех или иных причин (например, под воздействием неожиданного толчка) объект может выйти из рабочего состояния x 1 и оказаться в некотором другом состоянии x 0 . При этом точка x 0 , в которую может попасть объект, заранее не известна, и мы должны уметь так управлять объектом, чтобы из любой точки x 0 (или хотя бы из точек x 0 достаточно близких к x 1 ) вернуть его в рабочее состояние x 1 (рис. 6).
 Такое управление часто осуществляется человеком (оператором), который следит за приборами и старается выбирать управление, поддерживающее объект в требуемом рабочем режиме.
Такое управление часто осуществляется человеком (оператором), который следит за приборами и старается выбирать управление, поддерживающее объект в требуемом рабочем режиме.
Однако в современных условиях высокого развития техники оператор зачастую не может успешно справиться с этой задачей ввиду сложности поведения объекта, большой быстроты протекания процессов и т. п. Поэтому чрезвычайно важно создать такие приборы, которые сами, без участия человека, управляли бы работой объекта (например, в случае выхода объекта из рабочего состояния возвращали бы его в это рабочее состояние). Такие приборы («регуляторы», «автоматические управляющие устройства» и т. п.) сейчас очень распространены в технике, их изучением занимается теория автоматического управления.
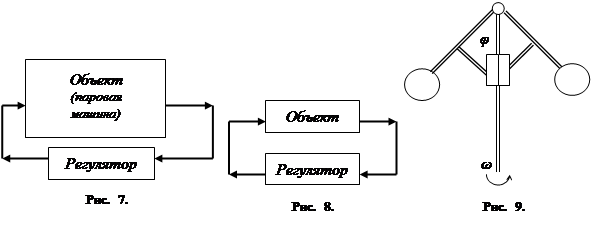
Первым устройством этого рода был центробежный регулятор Уатта, сконструированный для управления работой паровой машины (см. рис. 9). Схема этого регулятора показана на рис. 7. В общем случае (рис. 8) на вход регулятора подаются фазовые координаты объекта.
 |
?????? ?????????, ????? переходный процесс (?. ?. ??????? ???????? ?? ?????????? ???????? ????????? x 0 ? ???????????? ????????? x 1 , ???. 5) ??? ? ???????????? ?????? ???????????, ????????, ????? ????? ???????? ???? ?????????? ??? ????? ???????, ??????????? ? ??????? ??????????? ????????, ???? ??????????? ? ?. ?. ????? ??????????? ?????????? ??????? ?????????? оптимальным процессом . ?????? ???????????? ???????? ??????? ?????????, ?. ?. ?????????? ??????????, в каком смысле ?????????? ?????????????. ???? ???? ???? ? ?????????? ??????? ????????, ?? ????? ???????? ?????????? оптимальными в смысле быстродействия . ????? ??????, ???????, ? ?????????? ???????? ?????? ????????? ?? ????? x 0 ? ????? x 1 (???. 5), ?????????? ??????????? ? ?????? ??????????????, ???? ?? ?????????? ????????, ???????????? ?????? ?? x 0 ? x 1 ?? ??????? ????? (????? ? ????? ??????????????, ??? x 1 ≠x 0 ). ??????????, ??????????, ????? ????????? ?? ?????? ????????? ?????? ? ??????? ?????????, ? ????? ??? ????????? ???????, ????????, ? ?????? ?????????????? (?. ?. ????????? ?????? ? ??????? ????????? ?? ?????????? ?????). ? ????? ? ???? ? ?????? ??????????????? ?????????? ??????????????? ?????? ????????? ??????????. ???????????? ??????????? ???????? ? ????, ??? ?????????? ??????? ??????????? ???????? ??????? ? ??????????? ??????????? ??????????; ???????, ???????? ??????????? ??????????, ????? ???? ???????????? ? ????????????, ?????????????? ??????????, ??????? ?? ???? ??????? ???????????? ?????????? ??????? ?? ?????????? ?????. ? ???????? ?? ?????????????? ??????????, ??-????????, ??????????? ??????. ?????? ????? ????? ???????? ?????????, ?. ?. ?????? ??? ??????? ?????????????? ???????, ?????????????? ????? ??????????. ????? ????????????, ??? ??????????? ?????????? ????? ?????? ?????? ???? ? ??????? ????????.
3. 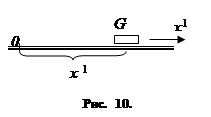 Уравнения движения объекта. Начнём с рассмотрения одного простого примера. Пусть G – тело, которое может совершать прямолинейное движение (рис. 10). Массу этого тела будем предполагать постоянной и равной m , а его размерами будем пренебрегать (т. е. будем считать G материальной точкой.) Координату тела G (отсчитываемую от некоторой точки O той прямой, по которой оно движется) будем обозначать через x 1 . При движении тела G его координата x 1 меняется с течением времени. Производная
Уравнения движения объекта. Начнём с рассмотрения одного простого примера. Пусть G – тело, которое может совершать прямолинейное движение (рис. 10). Массу этого тела будем предполагать постоянной и равной m , а его размерами будем пренебрегать (т. е. будем считать G материальной точкой.) Координату тела G (отсчитываемую от некоторой точки O той прямой, по которой оно движется) будем обозначать через x 1 . При движении тела G его координата x 1 меняется с течением времени. Производная ![]() представляет собой скорость движения тела G . Будем предполагать, что на тело G действуют две внешние силы: сила трения ─
представляет собой скорость движения тела G . Будем предполагать, что на тело G действуют две внешние силы: сила трения ─![]() и упругая сила ─ kx 1 и что, кроме того, тело G снабжено двигателем. Развиваемую двигателем силу воздействия на тело G обозначим через u . Таким образом, по второму закону Ньютона движение телаG с течением времени будет описываться дифференциальным уравнением
и упругая сила ─ kx 1 и что, кроме того, тело G снабжено двигателем. Развиваемую двигателем силу воздействия на тело G обозначим через u . Таким образом, по второму закону Ньютона движение телаG с течением времени будет описываться дифференциальным уравнением
![]()
Обозначив скорость движения через x2 (т. е. положив ![]() ), мы сможем записать этот закон движения в виде следующей системы дифференциальных уравнений:
), мы сможем записать этот закон движения в виде следующей системы дифференциальных уравнений:
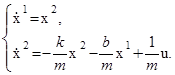 (1.1)
(1.1)
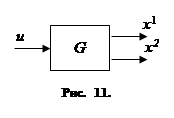
Здесь величины x 1 , x 2 являются фазовыми координатами тела G , а величина u – управляющим параметром, т. е. мы имеем объект, схематически изображённый на рис. 11.
Уравнения (1.1) представляют собой закон изменения фазовых координат с течением времени (с учётом воздействия управляющего параметра), т. е. представляют собой закон движения фазовой точки в фазовой плоскости.
Мы рассмотрели лишь один частный случай, но можно было бы указать целый ряд других примеров, в которых закон движения объекта описывается дифференциальными уравнениями. Чаще всего (см.(1.1)) эти уравнения дают выражения производных от фазовых координат через сами фазовые координаты и управляющие параметры, т. е. имеют вид
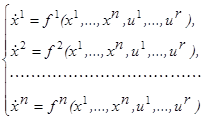 (1.2)
(1.2)
где f 1 , f 2 ,…, fn – некоторые функции, определяемые внутренним устройством объекта.
В дальнейшем мы сосредоточим своё внимание именно на таких объектах (рис. 2), закон движения которых описывается системой дифференциальных уравнений вида (1.2). В векторной форме систему (1.2) можно записать в виде
![]() (1.3)
(1.3)