Реферат: Синтез оптимальных уравнений
(см. (1.2), (1.3)) и начальному условию
y (t 0 )=x 0 . (1.10)
Если мы будем двигаться из точки x 0 до точки y( t ) (по рассматриваемой фазовой траектории), то затратим на это движение время t ─ t 0 . Двигаясь затем из точки y( t ) оптимально, мы затратим на движение от точки y (t ) до точки x 1 время T( y( t )). В результате мы совершим переход из точки x 0 в точку x 1 , затратив на этот переход время (t ─t 0 )+T (y (t)). Но так как оптимальное время движения от точки x 0 до точки x 1 равно T (x 0 ), т. е. равно T (y (t 0 )), то T (y(t 0 ))≤(t ─t 0 )+T (y (t )). Заменяя функцию T через ω (см. (1.8)) и разделив обе части неравенства на положительную величину t ─t 0 , получаем отсюда ![]() и поэтому, переходя к пределу при t→ t 0 , находим
и поэтому, переходя к пределу при t→ t 0 , находим
![]() │при
│при ![]() ≤1. (1.11)
≤1. (1.11)
Но производная, указанная в левой части этого неравенства, вычисляется по формуле полной производной 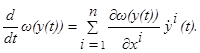 Поэтому согласно (1.9) и (1.10) неравенство (1.11) принимает вид
Поэтому согласно (1.9) и (1.10) неравенство (1.11) принимает вид  Точки x 0 , u 0 здесь были произвольными. Таким образом, для любой (отличной от x 1 ) точки x фазового пространства и любой точки u области управления U выполнено соотношение
Точки x 0 , u 0 здесь были произвольными. Таким образом, для любой (отличной от x 1 ) точки x фазового пространства и любой точки u области управления U выполнено соотношение
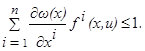 (1.12)
(1.12)
Пусть теперь (u (t ), x (t )) ─ оптимальный процесс, переводящий объект из фазового состояния x 0 в состояние x 1 , и t 0 ≤t ≤t 1 ─ отрезок времени, в течение которого это оптимальное движение происходит, так что x (t 0 )=x 0 , x (t 1 )=x 1 и t 1 =t 0 + T (x 0 ). Движение по рассматриваемой оптимальной траектории от точки x 0 до точки x (t ) осуществляется в течение времени t ─t 0 , а движение от точки x (t ) до точкиx 1 ─ в течение времени T (x 0 ) ─ (t ─t 0 ). Быстрее, чем за время T (x 0 ) ─ (t ─t 0 ), из точки x (t ) попасть в точку x 1 невозможно. Итак, T (x 0 ) ─ (t ─t 0 ) есть время оптимального движения из точки x (t ) в точку x 1 , т. е. T (x (t ))=T (x 0 ) ─ (t ─t 0 ). Заменив здесь T через ω , т. е. ω (x (t ))=ω (x 0 ) + t ─t 0 ) и взяв производную по t , получаем
 t 0 ≤t ≤t 1 . (1.13)
t 0 ≤t ≤t 1 . (1.13)
Таким образом, для каждого оптимального процесса в течение всего движения выполняется равенство (1.13).
Если мы теперь введём в рассмотрение функцию
B (x, u (t ))= , (1.14)
, (1.14)
То соотношения (1.12) и (1.13) могут быть записаны следующим образом:
B (x, u )≤1 для всех точек x ≠x 1 и u ; (1.15)
B (x, u )≡1 для любого оптимального процесса (u (t ), x (t )). (1.16)
Итак, справедлива следующая
Т е о р е м а 1.1. Если для управляемого объекта, описываемого уравнением (1.5) и предписанного конечного состояния x 1 выполнены гипотезы 1 и 2, то имеют место соотношения (1.15) и (1.16) (оптимальность понимается в смысле быстродействия).
Эта теорема и составляет сущность метода динамического программирования для рассматриваемой задачи. Эту теорему можно сформулировать и несколько иначе. Написав соотношение (1.16)
Для t =t 0 , получим B (x 0 , u (t 0 ))=1, т. е. для любой точки x 0 (отличной от x 1 ) найдётся в U такая точка u (а именно u= u (t 0 )), что B (x 0 , u )=1. В сопоставлении с неравенством (1.15) получаем соотношение
 для любой точки x ≠x 1 . (1.16* )
для любой точки x ≠x 1 . (1.16* )
Метод динамического программирования (1.15), (1.16) (или, что то же самое, (1.16* ), (1.16)) содержит некоторую информацию об оптимальных процессах и потому может быть использован для их разыскания. Однако он имеет ряд неудобств. Во-первых, применение этого метода требует нахождения не только оптимальных управлений, но и функции ω (x ), так как эта функция входит в соотношения (1.15) ─ (1.16* ). Во-вторых, уравнение Беллмана (1.16* ) (или соотношения (1.15), (1.16)) представляет собой уравнение в частных производных относительно функции ω , осложнённое к тому же знаком максимума. Указанные обстоятельства сильно затрудняют возможность пользования методом динамического программирования для отыскания оптимальных процессов в конкретных примерах. Но самым главным недостатком этого метода является предположение о выполнении гипотез 1 и 2. Ведь оптимальные управления и функция ω нам заранее не известны, так что гипотезы 1 и 2 содержат предположение о неизвестной функции, и проверить выполнение этих гипотез по уравнениям движения объекта невозможно. Этот недостаток можно было бы считать не особенно существенным, если бы после решения оптимальной задачи этим методом оказалось, что функция ω (x ) действительно является непрерывно дифференцируемой. Но дело заключается в том, что даже в простейших, линейных задачах оптимального управления функция ω (x ) не является, как правило, всюду дифференцируемой. Тем не менее, методом динамического программирования можно нередко пользоваться как ценным эвристическим средством.
6. Принцип максимума. Продолжим теперь рассуждения предыдущего пункта, предположив функцию ω (x ) уже дважды непрерывно дифференцируемой (всюду, кроме точки x 1 ). Итак, будем предполагать, что выполнена следующая
Г и п о т е з а 3. функция ω (x ) имеет при x≠ x 1 вторые непрерывные производные  i, j= 1,2,…,n , а функции fi (x, u ) ─ первые непрерывные производные
i, j= 1,2,…,n , а функции fi (x, u ) ─ первые непрерывные производные  где i, j= 1,2,…,n.
где i, j= 1,2,…,n.
Пусть (u( t), x( t) ), t 0 ≤t ≤t 1 , ─ оптимальный процесс, переводящий объект (1.2) (или (1.3)) из фазового состояния x 0 в состояние x 1 . Фиксируем некоторый момент времени t , t 0 ≤t ≤t 1 , и рассмотрим функцию B (x, u (t ))= переменного x. В силу гипотезы 3 вытекает, что функция B (x, u (t )) всюду, кроме точки x 1 , имеет непрерывные производные по переменным x 1 ,x 2 ,…,xn :
переменного x. В силу гипотезы 3 вытекает, что функция B (x, u (t )) всюду, кроме точки x 1 , имеет непрерывные производные по переменным x 1 ,x 2 ,…,xn :
 (1.17)
(1.17)
В частности, так как x (t )≠x 1 (поскольку t <t 1 ), то функция B (x, u (t )) имеет вблизи точки x =x (t ) непрерывные производные по переменным x 1 ,x 2 ,…,xn . Далее, мы имеем в силу (1.15), (1.16) B (x, u (t ))≤1 для любого x≠ x 1 ; B (x, u (t ))=1 при x= x (t ).
Эти два соотношения означают, что функция B (x, u (t )) достигает в точке x =x (t ) максимума, и потому её частные производные по x 1 ,…, xn обращаются в нуль в этой точке:
 (1.18)
(1.18)
Кроме того, дифференцируя функцию ![]() по t, находим
по t, находим
