Реферат: Синтез управляющего автомата модели LEGO транспортной тележки и моделирование ее движения
Таблица 5.5 – Таблица истинности комбинационной схемы автомата
| S[j] | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| Y0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 |
| Y1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | 1 |
| S[j+1] | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| X0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| X1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 |
| X2 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
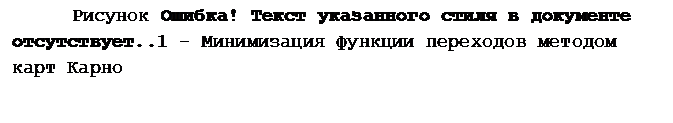
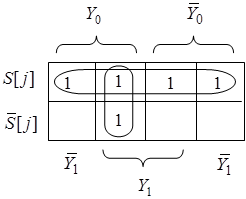 |
5.7 Теперь можно записать логические выражения для комбинационной схемы автомата.
Функция переходов:
![]() . (5.1)
. (5.1)
Функции выходов в СДНФ по таблице истинности:
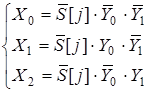 . (5.2)
. (5.2)
Для удобства реализации комбинационной схемы представим рассматриваемые функции в базисе “ИЛИ-НЕ”:
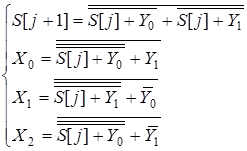 . ( 5.3)
. ( 5.3)
5.8 На основе системы (5.3), окончательно получаем цифровую схему реализации управляющего автомата транспортной тележки, представленную на рисунке 5.2.
Особенностью полученной схемы является то, что она не содержит элементы памяти и задержки и, соответственно, не является тактируемой. Такой вариант реализации возможен для автоматов с двумя состояниями, одно из которых является абсолютно устойчивым. В нашем случае состояние блокировки есть абсолютно устойчивое состояние. Если комбинационная схема сформируем это состояние, то за счёт обратной связи по линии S запрещается реакция выходов X на изменение входных сигналов Y. Выход из этого устойчивого состояния возможен только принудительным обнулением линии S единичным уровнем на линии “Сброс”. Конфликтных “Состязаний” в рассматриваемом автомате не возникает.

6 Решение дополнительного задания
6.1 Действующая на тележку в динамике система сил раскладывается на результирующую силу, приложенную к центру масс тележки 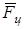 и вращающий момент
и вращающий момент 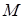 , относительно того же центра масс.
, относительно того же центра масс.
6.2 Как видно из рисунка 1.1 вращающий момент определяется только силой реакции опоры переднего колеса 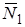 —
—
![]() , (6.1)
, (6.1)
где ![]() — угол поворота переднего колеса.
— угол поворота переднего колеса.
Зная из рисунка, что
![]() , ( 6.2)
, ( 6.2)
получим:
![]() . ( 6.3)
. ( 6.3)
Положительные значения вращающего момента соответствуют повороту тележки влево, отрицательные — вправо.
6.3 Результирующая сила, действующая на центр масс тележки, определяется векторной суммой всех сил на рисунке 1.1:
![]() . ( 6.4)
. ( 6.4)
Для нашего случая важно знать направление действия силы ![]() , которое зависит от направлений и величин составляющих рассматриваемой суммы. В свою очередь направления составляющих рассматриваются относительно положения габаритной определяющей, которое характеризуется единичным вектором:
, которое зависит от направлений и величин составляющих рассматриваемой суммы. В свою очередь направления составляющих рассматриваются относительно положения габаритной определяющей, которое характеризуется единичным вектором:
![]() , ( 6.5)
, ( 6.5)
где ![]() — вектор, задающий координаты центра масс тележки;
— вектор, задающий координаты центра масс тележки;
![]() — вектор, задающий координаты точки приложения силы тяги
— вектор, задающий координаты точки приложения силы тяги ![]() ;
;
![]() — габаритная определяющая транспортной тележки.
— габаритная определяющая транспортной тележки.
6.4 Вектор 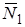 представляется в базисе вектора
представляется в базисе вектора 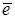 следующим образом:
следующим образом:
![]() , (6.6)
, (6.6)
где ![]() — единичный вектор, ортогональный вектору
— единичный вектор, ортогональный вектору ![]() ,
,
или
![]() . (6.7)
. (6.7)
Если ![]() имеет координаты
имеет координаты ![]() , то
, то ![]() имеет координаты
имеет координаты ![]() . Тогда вектор
. Тогда вектор ![]() , выраженный в базисе Декартовой системы координат, имеет вид:
, выраженный в базисе Декартовой системы координат, имеет вид:
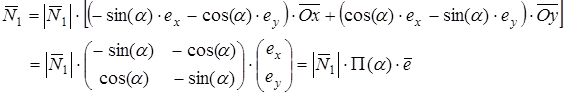 , (6.8)
, (6.8)