Реферат: Система автоматического регулирования температуры газов в газотурбинном двигателе
D2 = =а1· а2 -а0· а3 =4,1-18,15=-14,05<0
=а1· а2 -а0· а3 =4,1-18,15=-14,05<0
Следовательно, замкнутая система не устойчива.
2)САУ с корректирующим звеном.
На этом этапе лабораторной работы рассматривается данная система, но уже с корректирующим звеном, для которого мы экспериментальным путём подбираем коэффициент коррекции, при котором система была бы устойчивой. Рассматривается два варианта, при k=0,1 и k=2.
а) Структурная схема:

|
График зависимости показывает, что система не устойчива.![]()
Передаточная функция:
![]()
где ![]() – характеристическое уравнение,
– характеристическое уравнение,
в котором а0 =3, а1 =4, а2 =1, а3 =5,5
Исследуем устойчивость системы с помощью критерия устойчивости Гурвица:
D1 =а1 =3>0,
D2 = =а1 ·а2 -а0 ·а3 =4,1·1-5,5·3,3=4,1-18,15<0
=а1 ·а2 -а0 ·а3 =4,1·1-5,5·3,3=4,1-18,15<0
Отсюда можно сделать вывод, что при значении коэффициента k=0,1 система не устойчива.
2)
|
График зависимости показывает, что система не устойчива.
Передаточная функция:
![]()
где ![]() – характеристическое уравнение,
– характеристическое уравнение,
в котором а0 =1,8, а1 =3,9, а2 =1, а3 =5,5
Исследуем устойчивость системы с помощью критерия устойчивости Гурвица:
D1 =а1 =1,8>0,
D2 = =а1 ·а2 -а0 ·а3 =3,9·5,5-1·1,8=19,65<0
=а1 ·а2 -а0 ·а3 =3,9·5,5-1·1,8=19,65<0
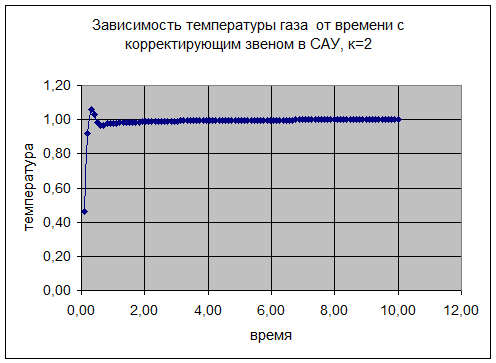
Отсюда можно сделать вывод, что при значении коэффициента К=2 система устойчива.
Вывод:
В данной лабораторной работе рассматривалась САУ регулирования температуры газов, поверялась ее устойчивость в зависимости от структуры.
В первом случае моделировалась разомкнутая САУ. Результаты исследования показали, что она находится на границе устойчивости (температура газа в газотурбинном двигателе непрерывно росла с течением времени), что указывает на ненадежность системы, так как она может в любой момент перейти в неустойчивое состояние.
Для повышения надежности системы вводится обратная отрицательная связь. Однако система оставалась неустойчивой, т.е. температура газа колебалась.