Реферат: Система натуральных чисел. Принцип математической индукции. Теоремы математической индукции

- истина.

(- истины®- истина).

Тогда предикат тождественно истинен на .

Теорема 4. (обобщение сильной формы принципа полной математической индукции). Пусть - одноместный предикат на , где , который удовлетворяет условиям:

- истина.

(- истины ®- истина).

Тогда предикат тождественно истинен на .

Числа Фибоначчи

Определение. Числа Фибоначчи , для , определяются рекуррентно

(1) , ;

для всех .

Из определения чисел Фибоначчи следует, что

, , , , , , , , , , .

Для вычисления чисел Фибоначчи справедлива следующая формула Бине

(3) , .

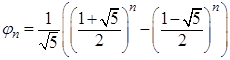Из (1) и (2) следует, что индукционное предположение, при доказательстве формулы Бине, должно предполагать справедливость (3) для и , и значит, начальные условия должны требовать выполнение (3) для и . Поэтому доказательство формулы Бине может проводиться по следующей теореме математической индукции.

Теорема 5. Пусть - одноместный предикат на , который удовлетворяет условиям:

- истины.

(- истины ®- истина).

Тогда предикат тождественно истинен на .

Проведём доказательство формулы Бине по теореме 5.

Для и равенство (3) принимает вид

, .

Очевидно, что эти равенства верны.

Предположим, что равенство (3) истинно для чисел и . Тогда из (2) следует, что

.

После простых преобразований правой части получим, что

По индукции формула Бине доказана.