Реферат: Система уравнений по формулам Крамера

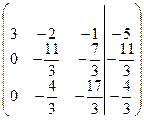
Второе уравнение умножим на 3, третье уравнение умножим на 3

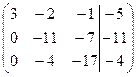
второе уравнение умножаем на 4/11 вычитаем третье.

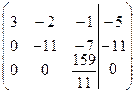
Первое уравнение разделим на 3

Второе уравнение разделим на -11

третье уравнение разделим на 159/11

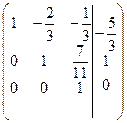
полученной матрице соответствует система уравнений

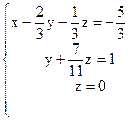
решаем уравнение снизу вверх

решение системы

Задание № 2

Координаты вершин пирамиды А(1, -4, 0), В(5, 0, -2), С(3, 7, -10), Д(1, -2, 1) – вершины пирамиды. Найти:

1) записать векторы АВ, АС, АД в системе орт и найти их длины

2) найти угол между векторами АВ и АС

3) найти проекцию вектора АД на вектор АВ

4) найти площадь грани АВС

5) найти объем пирамиды АВСД

Решение

1. записать векторы в системе орт и найти их длины.

Произвольный вектор может быть представлен в системе орт i, j, k следующей формулой , где - проекции вектора а на соответствующие координатные оси. Если даны точки и , то проекции вектора на координатные оси находятся по формулам

; ;

расстояние между двумя точками и определяется по формуле