Реферат: Случайные величины и способы их описания Основные понятия теории вероятности применяемые при
Министерство образования Республики Беларусь
Белорусский государственный университет информатики и
радиоэлектроники
кафедра РЭС
РЕФЕРАТ
на тему:
«Случайные величины и способы их описания. Основные понятия теории вероятности, применяемые при испытаниях РЭСИ»
МИНСК, 2008
Случайные величины и способы их описания
Случайные величины могут быть:
• дискретными (если количество возможных значений конечно);
• непрерывными.
Характеристикой случайной величины является закон распределения, т.е. связь между возможными значениями случайной величины и соответствующими их вероятностями.
Для непрерывных случайных величин используют четыре способа аналитического описания законов распределения:
• плотность распределения f(x);
• интегральная функция распределения ![]()
• обратная интегральная функция распределения ![]()
• функция интенсивности 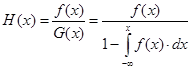
Соответствующие графические зависимости
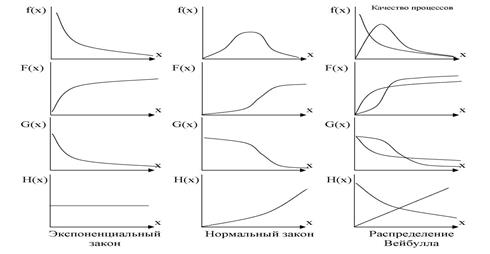
Рисунок 1 - Графические зависимости законов распределения
Таким образом, распределения случайных величин Т, Тв , Тс , Тд , задаваемые в любой из возможных форм, являются характеристиками надежности (безотказности, ремонтопригодности, сохраняемости и долговечности).
Широко используются в инженерной практике различные численные показатели надежности (показатели безотказности, сохраняемости, долговечности, ремонтопригодности). В качестве таких показателей используются числовые характеристики соответствующих случайных величин.
Наиболее широко используются математические ожидания:
• среднее время безотказной работы Т;
• среднее время восстановления Тв ;
• среднее время сохраняемости Тс ;
• средний срок службы Тс.с ;
• средний ресурс Тр и другие показатели.
Приведем основные показатели для восстанавливаемой и невосстанавливаемой аппаратуры.
Таблица 1 - Основные показатели для восстанавливаемой и невосстанавливаемой аппаратуры
| Составля- | Случайная | Математическая | Показатели | надежности | |||
| ющая | величина | модель | Невосстанав- | Восстанавлива- | |||
| надежности | распределения | ливаемая | емая | ||||
| Безотказ- | Время | Экспоненциаль- | Т- среднее | Т- наработка на | |||
| ность | безотказной | ное | время | отказ. | |||
| работы Т | Нормальное | безотказной | Р(t)- | ||||
| Гамма | работы. | вероятность | |||||
| Р(t)- | безотказной | ||||||
| вероятность | работы. | ||||||
| безотказной | λ,- параметр | ||||||
| работы за | потока отказов | ||||||
| заданное | |||||||
| время. | |||||||
| λ,- интенсив- | |||||||
| ность отказов | |||||||
| Ремонто- | Время | Эрланга | Тв - среднее | ||||
| пригод- | восстанов- | Нормальное | время | ||||
| ность | ления | Экспоненциаль- | восстановления. | ||||
| Тв | ное | FB (τ)- | |||||
| вероятность | |||||||
| восстановления | |||||||
| работоспособ- | |||||||
| ности отказав- | |||||||
| ших изделий за | |||||||
| заданное время. | |||||||
| Сохраня- | Время | Нормальное | Те же, что и | Тс - среднее | |||
| емость | хранения | Логарифмичес- | для восстанав- | время | |||
| до потери | ки-нормальное | ливаемой. | сохраняемости. | ||||
| изделием | Гамма | Gc (τ)- | |||||
| своих | Вейбула | вероятность | |||||
| характе- | Экспоненциаль- | сохранения | |||||
| ристик Тс | ное | технических | |||||
| характеристик | |||||||
| в течении | |||||||
| задан-ного | |||||||
| времени | |||||||
| τGt -гамма- | |||||||
| процентный | |||||||
| срок | |||||||
| сохраняемости | |||||||
| Долговеч- | Время от | Нормальное | Показатели, | Тс .с -средний | |||
| ность | начала | Логарифмически- | как и для | срок службы. | |||
| эксплуата- | нормально | показателей | Тр -средний | ||||
| ции до | Гамма | безотказности. | ресурс. | ||||
| предель- | Вейбула | Tc .с.j - гамма- | |||||
| ного сос- | Экспоненциаль- | процентный | |||||
| тояния Тд | ное | срок службы | |||||
| Тс .с. - срок | Gcc (τ)- | ||||||
| службы. | вероятность | ||||||
| Тр -техни- | того, что срок | ||||||
| ческий | службы образца | ||||||
| ресурс. | превысит | ||||||
| зоданное время. | |||||||
| Gp (τ)- | |||||||
| вероятность | |||||||
| того, что ресурс | |||||||
| изделия | |||||||
| превысит τ | |||||||
Для количественной оценки безотказности по результатам испытаний наиболее часто используют следующие характеристики:
• вероятность безотказной работы изделия на момент времени t.
Характер изменения вероятности безотказной работы РЭСИ от времени выглядит следующим образом:
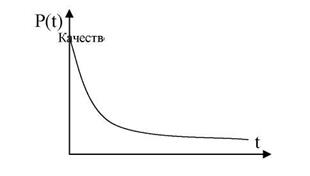
Рисунок 2 - Характер изменения вероятности безотказной работы РЭСИ от времени
Площадь, ограниченная функцией P(t) и осями координат численно равна средней наработке изделия до отказа. При заданной min вероятности безотказной работы Р2
--> ЧИТАТЬ ПОЛНОСТЬЮ <--