Реферат: Спектральные характеристики
Итак, ![]() - аналитическая оператор-функция на множестве регулярных точек (резольвентном множестве).
- аналитическая оператор-функция на множестве регулярных точек (резольвентном множестве). ![]() - разложение в ряд Лорана (имеет место при
- разложение в ряд Лорана (имеет место при ![]() , но, возможно, и в большей области).
, но, возможно, и в большей области).
Упражнение: (Примеры вычисления спектрального радиуса)
![]() ,
,
![]()
![]() .
.
Возьмем![]() .Тогда
.Тогда
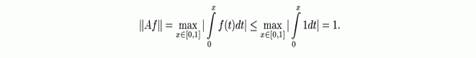
Таким образом ![]() . Эта оценка достижима при
. Эта оценка достижима при ![]() , т.е.
, т.е. ![]() ,и rc (A) =1.
,и rc (A) =1.
Теорема 4: всякая к.ч ![]() , есть регулярная точка самосопряженного оператора A.
, есть регулярная точка самосопряженного оператора A.
Доказательство.
]![]() регулярная точка, значит
регулярная точка, значит ![]() не собственное значение и
не собственное значение и ![]() . Проверим ограниченность
. Проверим ограниченность ![]() .
.
![]()
![]()
![]()
![]()
![]() ограничен,
ограничен, ![]() и его можно распространить на
и его можно распространить на ![]() с сохранением нормы оператора, так как
с сохранением нормы оператора, так как ![]() не собственое значение. Если при этом
не собственое значение. Если при этом ![]() не замкнуто, то
не замкнуто, то ![]() не замкнут. При этом линейный оператор, обратный к замкнутому, а также сопряженный к нему, замкнут => самосопряженный оператор замкнут.
не замкнут. При этом линейный оператор, обратный к замкнутому, а также сопряженный к нему, замкнут => самосопряженный оператор замкнут.
Спектральная теория в электронике
Полезнейшим приложением спектральной теории в физике является теория спектров электрических сигналов. Суть теории состоит в том, что любой сигнал на входе линейной цепи возможно представить совокупностью гармонических колебаний, или тестовых сигналов, заданной частоты, вопрос такого разложения состоит в нахождении амплитуд результирующих колебаний. Последние вычисляются определенным образом.
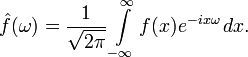
Классическое преобразование Фурье представляет из себя линейный оператор.
Спектральная теория здесь работает следующим образом – для периодических входных сигналов для нахождения соответствующих амплитуд используется интегральное преобразование – дискретный Фурье- образ:
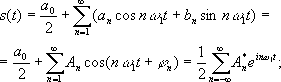
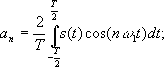
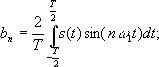
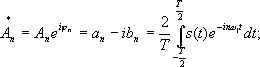
в котором разложение начинается с частоты следования wк . В данном случае очевидно, что, раз выходной сигнал представляется суммой бесконечного ряда, то мы имеем дело с точечным спектром сигнала , поскольку он дискретен. Следовательно, любое периодическое колебание можно рассматривать как сигнал с дискретным спектром, поскольку непрерывным спектром он не обладает. Однако, если же взять непериодический сигнал, например, единичный прямоугольный импульс, то вводится понятия прямого и обратного преобразований Фурье :
![]()
![]() ,
,
где S(w) – спектральная плотность сигнала s(t).
Соответственно, S(w) – непрерывная по w функция, и в данном.
Заключение
В работе не ставилась цель охватить весь курс спектральной теории и спектрвльных характеристик, а ставилась цель изучить основные спектральные характеристики линейных операторов, и обрисовать применение этих понятий. Опять же, класс Фурье преобразований включает в себя намного больший объем, чем тот, о котором упомянуто в работе, они используются в теории алгоритмов при кодировке и сжатии информации в цифровом формате изображений JPEG, в вейвлет - преобразованиях. Новое поколение функциональной электроники содержит на элементарном уровне элементы, способные производить непрерывные преобразования Фурье и Лапласа, что намного ускоряет работу электронных устройств.
В общем и целом, наряду с первой частью работа дает представление о б основных спектральных характеристиках линейных операторов и их применении в различных областях математики, информатики и физики.
Список литературы