Реферат: Способи перетворення креслення

Задача 3. Перетворити креслення так, щоб площина загального положення в новій системі площин проекцій стала проекціюючою.

Нехай площина загального положення задана трьома точками А, В, С (рис. 4). Для розв’язування сформульованої задачі нову площину проекцій потрібно розташувати перпендикулярно трикутнику ABC і одній з площин проекцій. Нова площина має бути перпендикулярна лінії перетину заданої площини з однією з площин проекцій. При цьому немає необхідності будувати таку лінію, оскільки її напрям можна встановити за допомогою головної лінії площини.

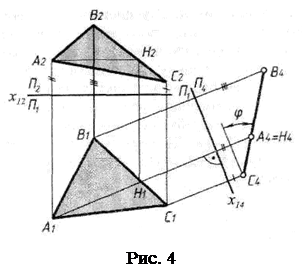
Ось чому в заданій площині перш за все проводять одну з головних ліній, наприклад горизонталь АН. Ця горизонталь потрібна для орієнтування нової площин проекцій р ₄ .

Розташувавши р₄ ^ АН, ми забезпечуємо виконання двох умов одразу: нова площина р₄ буде перпендикулярна і до р₁ і до площини трикутника. Нову вісь х₂₄ проводять під прямим кутом до А₁ Н₁ . Провівши через горизонтальні проекції вершин трикутника прямі, перпендикулярні до нової осі, відкладають на них від х₁₄ відрізки, що дорівнюють z_A , z_B і z_С . Так одержують нову фронтальну проекцію А₄ В₄ С₄ трикутника ABC, яка являє собою пряму лінію. Відмітимо, що на площину р₄ , яка перпендикулярна до трикутника і р₁ , без спотворення проекціюється кут ц, утворений трикутником з площиною р₁ .

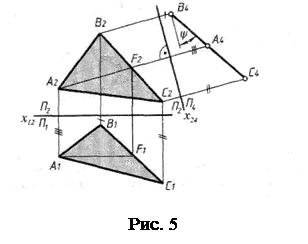
Аналогічне перетворення виконано на рис. 5, де площина р₁ замінена площиною р₄ , перпендикулярною до р₂ і трикутника ABC. Для цього в площині трикутника була проведена фронталь AF, перпендикулярно до якої і розташовується площина р₄ . Нова вісь х₂₄ вибрана перпендикулярно до A₂ F₂ . Площина трикутника відносно р₁ стала проекціюючою. На площину р₄ без спотворення проекціюється кут y нахилу трикутника до фронтальної площини проекцій р₂ .

Задача 4. Перетворити креслення так, щоб площина загального положення стала паралельною одній з площин проекцій нової системи

Нехай задано трикутник ABC у площині загального положення (рис. 6). Потрібно створити таку нову ортогональну систему площин проекцій, в якій одна з них має бути паралельною трикутнику. В системі р₂ / р₁ таку площину побудувати не можна. Справді, площина трикутника, не буде перпендикулярна ні до р₁ ні до р₂ , тобто вона не утворює з площинами проекцій ортогональної системи.

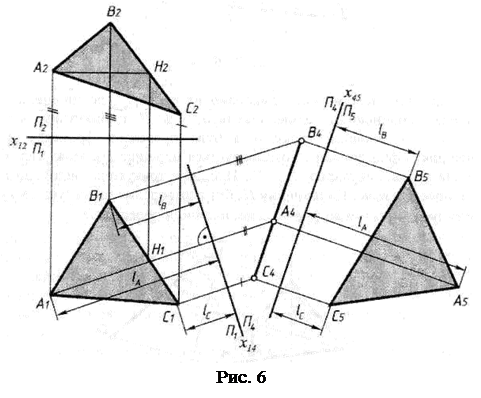
Розв’язування задачі потребує подвійної заміни площин проекцій. Суть першої заміни р₂ на р₄ полягає в перетворенні площини трикутника в проекціюючу площину. Цей процес описаний вище задачі № 3.

Другий етап розв’язування задачі полягає в переході від системи р₁ / р₄ до системи р₄ / р₅ . Нова площина р₅ установлюється паралельно трикутнику, а отже, нова вісь х₄₅ на епюрі проводиться паралельно прямій, на якій виявились розташованими точки А₄ , В₄ і С₄ . Як правило, через вказані точки проводять перпендикуляри до нової осі і відкладають на них від х₄₅ відрізки, що дорівнюють l_А , l_в , l_с . Побудована проекція А₅ В₅ С₅ визначає дійсну величину трикутника.

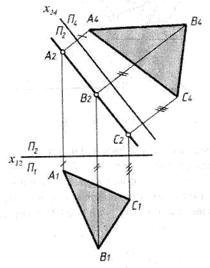
Якщо ж задана площина є проекціюючою (рис. 7), то розглядувана задача розв’язується однією заміною площин. В цьому випадку площина р₄ , паралельна трикутнику ABC, утворює з р₂ ортогональну систему р₂ / р₄ . Нова проекція А₄ В₄ С₄ на площину р₄ визначає дійсну величину трикутника.

Рис. 7

???????? ?? ??????? ???????

1. Задачі нарисної геометрії можна розділити на позиційні та метричні. В позиційних задачах треба знайти положення геометричних фігур. В метричних задачах треба знайти натуральні розміри геометричних фігур.

2. Існують два основних способи перетворення проекцій:

– спосіб заміни площин проекцій;

– спосіб обертання.

2. Способи обертання

Спосіб плоско-паралельного переміщення

Плоско-паралельним переміщенням називається такий рух фігури в просторі, при якому всі її точки переміщуються в площинах, паралельних між собою і паралельних однієї з площин проекцій.

Основні положення плоско-паралельного переміщення:

1) при плоско-паралельному переміщенні фігури відносно площини проекцій р₁ фронтальні проекції точок переміщуються по прямим, паралельним осі Ох, а горизонтальна проекція фігури залишається незмінною за своєю величиною і формою;

2) при плоско-паралельному переміщенні фігури відносно площини проекцій р₂ горизонтальні проекції точок переміщуються паралельно осі Ох, а фронтальна проекція фігури залишається незмінною за своєю величиною і формою.

Спосіб обертання навколо проекціюючою осі

Сутність цього способу полягає в тому, що система площин проекцій р₂ /р₁ залишається нерухомою, а положення геометричних елементів міняється шляхом обертання навколо однієї або двох обраних осей до потрібного положення в даній системі.

Цим способом вирішуються задачі на визначення: