Реферат: Спрос и рынок капитала

Поэтому на рис. 3.19 вспомогательная бюджетная прямая K'L' , параллельная KL ₁ , проводится не как касательная к прежней кривой безразличия U ₂ U ₂ , а строго через точку E ₁ , соответствующую оптимальному набору товаров X и Y при прежнем соотношении цен. Очевидно, она окажется касательной к более высокой, чем U ₂ U ₂ кривой безразличия U ₃ U ₃ , что означает и возможность достигнуть (в случае полной компенсации потребителю падения его покупательной способности) более высокого уровня удовлетворения, чем при использовании модели Хикса. Таким образом, общий результат повышения цены товара X (Х ₁ - Х ₂ ) разлагается на эффект замены (Х ₁ ≈ Х ₃ ) и эффект дохода (Х ₃ - Х ₂ ). Заметим, что движение от E ₁ к E ₂ происходит не вдоль кривой безразличия , как на рис. 3.16 и 3.17, а вдоль вспомогательной бюджетной прямой K'L'

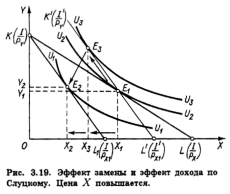
Сравнив два подхода, мы видим, что метод Хикса предполагает знание потребительских предпочтений, кривых безразличия, тогда как метод Слуцкого не требует этого, он базируется на наблюдаемых и регистрируемых фактах поведения потребителя на рынке.

ОБОБЩЕНИЕ

Различия в подходах Хикса и Слуцкого удобно рассмотреть, совместив их на одном рисунке (рис. 3.20).

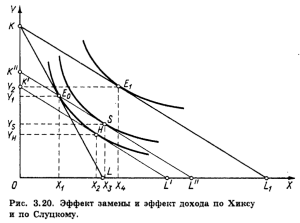
Здесь KL ≈ бюджетная прямая при номинальном доходе I и ценах Р_X и Р_Y , ее уравнение

XР_X + YР_Y =I ;

KL ₁ ≈ бюджетная прямая при том же номинальном доходе I и ценах Р_X + DР_X и Р_Y (причем DР_X - < 0), ее уравнение

X (Р_X + DР_X ) + YР_Y = I ;

E ₀ и E ₁ - комбинации товаров X и Y до и соответственно после снижения цены X ; K▓L▓ и K▓▓L▓▓ - вспомогательные соответственно по Хиксу и по Слуцкому. Их уравнения

I_H = X(Р_X + D Р_X ) + YР_Y |_{U = const}

I_S = X(Р_X + D Р_X ) + YР_Y |_{X, Y = const}

H и S- комбинации товаров X и Y, отвечающие требованию неизменного реального дохода соответственно по Хиксу и по Слуцкому.

Теперь мы можем представить методы разложения общего результата изменения цены Р_X по Хиксу и по Слуцкому в виде двух равенств:

(Х₄ - Х₁ ) = (Х₄ - Х₂ ) + (Х₂ - Х₁ ) (по Хиксу), (3.14)

(Х₄ - Х₁ ) = (Х₄ - Х₂ ) + (Х₂ - Х₁ ) (по Слуцкому). (3.15)

Левые части (3.14) и (3.15) характеризуют общий результат изменения цены Р_X в мере изменения объема спроса на товар X, и в обоих случаях они одинаковы. Правые части представляют суммы эффектов дохода и замены. Очевидно, что разница в распределении общего результата на эффект дохода и эффект замены составляет Х₃ ≈Х₂ - В (3.14) эта величина входит в эффект дохода, в (3.15) ≈ в эффект замены.

Можно показать, что величина Х₃ -Х₂ ╝ 0 при D Р_X ╝ 0, так что при малых изменениях Р_X подходы Хикса и Слуцкого дают практически одинаковый результат. ²

В дифференциальной форме равенства (3.14) и (3.15) имеют вид

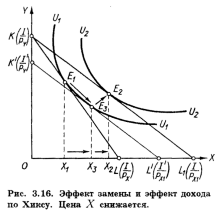
(по Хиксу)

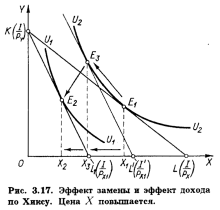
(по Слуцкому)

Левые части (3.16) и (3.17) одинаковы и представляют общий результат изменения Р_X при неизменных номинальном доходе I и цене Р_Y . Здесь d X/ d Р_X можно интерпретировать как наклон линии спроса на товар X, если Р_X принять как аргумент, а объем спроса ≈ как функцию.

Правые части представляют, как и в (3.14) и (3.15), суммы эффектов дохода и замены. При этом в (3.17) Х₁ = d I/ d Р_X , поскольку при изменении Р_X на D Р_X для приобретения прежнего товарного набора E₀ (Х₁ , Y₁ ) потребовалось бы компенсирующее изменение номинального дохода потребителя на Х₁ D Р_X , или в расчете на единицу изменения цены Х₁ D Р_X / D Р_X , т.е. Х₁ .

Эффект замены d Х/ d Р_X всегда отрицателен, так как цена и количество изменяются в противоположных направлениях.

Знак перед пер?