Реферат: Статистические методы изучения уровня и динамики себестоимости продукции 4

Компромиссом явился "идеальный индекс" Фишера:

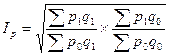
ГЛАВА 2.

РАСЧЕТНАЯ ЧАСТЬ

Имеются следующие выборочные данные по предприятиям одной из отраслей промышленности в отчетном году (выборка 20%-ная механическая):

№ пред-приятия п/п	Выпуск продукции, тыс.ед.	Затраты на производство продукции, млн. руб.	№ пред-приятия п/п	Выпуск продукции, тыс.ед.	Затраты на производство продукции, млн. руб
1	160	18,240	16	148	17,612
2	140	17,080	17	110	13,970
3	105	13,440	18	146	17,666
4	150	17,850	19	155	17,980
5	158	18,170	20	169	19,266
6	170	19,210	21	156	17,940
7	152	17,936	22	135	16,335
8	178	19,580	23	122	15,250
9	180	19,440	24	130	15,860
10	164	18,860	25	200	21,000
11	151	17,818	26	125	15,250
12	142	17,040	27	152	17,784
13	120	15,000	28	173	19,030
14	100	13,000	29	115	14,490
15	176	19,360	30	190	19,950

2.1. ЗАДАНИЕ 1

Признак – себестоимость единицы продукции (определите как отношение затрат на производство продукции к выпуску продукции).

Число групп – пять .

РЕШЕНИЕ

Для начала определим признак – себестоимость единицы продукции (х), как отношение затрат на производство продукции к выпуску продукции по формуле:

затраты на производство продукции

Себестоимость единицы продукции = выпуск продукции

Результаты расчетов приведем в таблице:

№ пред-приятия п/п	Выпуск продукции, тыс.ед.	Затраты на производство продукции, млн. руб.	Себестоимость единицы продукции, руб.	№ пред-приятия п/п	Выпуск продукции, тыс.ед.	Затраты на производство продукции, млн. руб	Себестоимость единицы продукции, руб.
1	160	18,240	114	16	148	17,612	119
2	140	17,080	122	17	110	13,970	127
3	105	13,440	128	18	146	17,666	121
4	150	17,850	119	19	155	17,980	116
5	158	18,170	115	20	169	19,266	114
6	170	19,210	113	21	156	17,940	115
7	152	17,936	118	22	135	16,335	121
8	178	19,580	110	23	122	15,250	125
9	180	19,440	108	24	130	15,860	122
10	164	18,860	115	25	200	21,000	105
11	151	17,818	118	26	125	15,250	122
12	142	17,040	120	27	152	17,784	117
13	120	15,000	125	28	173	19,030	110
14	100	13,000	130	29	115	14,490	126
15	176	19,360	110	30	190	19,950	105

Ранжируем ряд распределения предприятий по возрастанию:

№ пред-приятия п/п	Выпуск продукции, тыс.ед.	Затраты на производство продукции, млн. руб.	Себестоимость единицы продук ции, руб.	Ранг	№ пред-приятия п/п	Выпуск продукции, тыс.ед.	Затраты на производство продукции, млн. руб	Себестои мость единицы продук ции, руб.	Ранг
1	160	18,240	114	8	16	148	17,612	119	17
2	140	17,080	122	24	17	110	13,970	127	28
3	105	13,440	128	29	18	146	17,666	121	21
4	150	17,850	119	18	19	155	17,980	116	13
5	158	18,170	115	11	20	169	19,266	114	9
6	170	19,210	113	7	21	156	17,940	115	10
7	152	17,936	118	16	22	135	16,335	121	20
8	178	19,580	110	6	23	122	15,250	125	26
9	180	19,440	108	3	24	130	15,860	122	23
10	164	18,860	115	12	25	200	21,000	105	2
11	151	17,818	118	15	26	125	15,250	122	22
12	142	17,040	120	19	27	152	17,784	117	14
13	120	15,000	125	25	28	173	19,030	110	4
14	100	13,000	130	30	29	115	14,490	126	27
15	176	19,360	110	5	30	190	19,950	105	1

Расчет величины интервала iпроизведем по формуле:

,

где х_max – максимальная величина признака, x_min – минимальная величина признака.

руб.

Получаем следующие интервальные группы:

№ группы	Интервал, руб.
I	105-110
II	110-115
III	115-120
IV	120-125
V	125-130

Построим интервальный ряд распределения предприятий по себестоимости единицы продукции:

Таблица 1 .

Группировка предприятий по себестоимости единицы продукции в отчетном году

Группы предприятий по себестоимости единицы продукции	Число предприятий
105-110	3
110-115	6
115-120	9
120-125	6
125-130	6
ИТОГО	30

Интервальный ряд распределения предприятий показывает, что наибольшее число предприятий, то есть 9 из 30 (или 30% всех предприятий) имеют себестоимость единицы продукции от 115 до 120 руб.

Построим графики полученного ряда распределения. Графически определим значение моды и медианы.

Рис. 1. Гистограмма распределения предприятий по уровню себестоимости единицы продукции

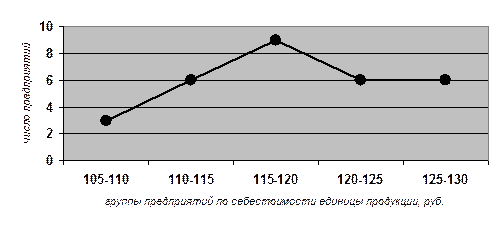
Рис. 2. Полигон распределения предприятий по уровню себестоимости единицы продукции

Для графического изображения медианы, построим кумуляту и рассчитаем кумулятивно накопленные частоты:

Группы предприятий по себестоимости единицы продукции	Кумулятивно накопленные частоты
105-110	3
110-115	9
115-120	18
120-125	24
125-130	30

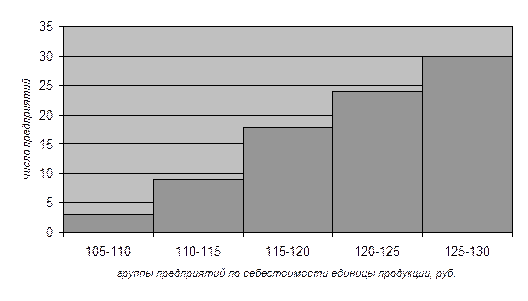
Рис. 3. Кумулята распределения предприятий по уровню себестоимости единицы продукции

Медиана, равная приблизительно 116,5 руб. показывает, что половина предприятий выборочной совокупности имеет себестоимость продукции меньше 116,5 руб., а другая половина больше 116,5 руб.

Мода, равная приблизительно 117,5 руб. показывает, что наиболее часто встречаются в совокупности предприятия со себестоимостью единицы продукции 117,5 руб.

Рассчитаем моду по следующей формуле

Мо = х о + i ,

где х о - нижняя граница модального интервала;