Реферат: Статистическое изучение основных фондов 2

Чтобы построить статистический ряд распределения организации, образовав пять групп с равными интервалами, определим величину интервала:

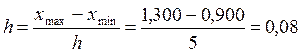(руб.)

Отсортированные данные

Таблица 2

№ предприятия п/п	Выпуск продукции	Среднегодовая стоимость основных производственных фондов	Фондоотдача
15	14,400	16,000	0,900
20	18,200	19,362	0,940
2	23,400	24,375	0,960
Всего	56,000	59,737	2,800
6	26,860	27,408	0,980
24	28,440	28,727	0,990
10	30,210	30,210	1,000
21	31,800	31,176	1,020
14	35,420	34,388	1,030
29	35,903	34,522	1,040
1	36,450	34,714	1,050
Всего	225,083	221,145	7,110
22	39,204	36,985	1,060
16	36,936	34,845	1,060
9	40,424	37,957	1,065
18	41,000	38,318	1,070
5	41,415	38,347	1,080
27	41,832	38,378	1,090
25	43,344	39,404	1,100
11	42,418	38,562	1,100
3	46,540	41,554	1,120
30	50,220	44,839	1,120
13	51,612	45,674	1,130
Всего	474,954	434,863	11,995
17	53,392	46,428	1,150
8	54,720	47,172	1,160
19	55,680	47,590	1,170
23	57,128	48,414	1,180
4	59,752	50,212	1,190
Всего	280,672	239,816	5,850
12	64,575	52,500	1,230
28	69,345	55,476	1,250
26	70,720	55,250	1,280
7	79,200	60,923	1,300
Всего	283,840	224,149	5,060

Таким образом, имеем следующее распределение предприятий по группам (таблица 3):

Распределение предприятий по группам

Таблица 3

№ п/п	Группа пред-тий по величине фондоотдачи	Число пред-тий	Сумма наблюдений
				1	0,900 – 0,980	3	3
2	0,980 – 1,060	7	10
3	1,060 – 1,140	11	21
4	1,140 – 1,220	5	26
5	1,220 – 1,300	4	30
Итого	30

1.2 В интервальном вариационном ряду мода вычисляется по формуле:

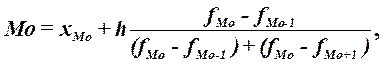
где х_Мo – нижняя граница модального интервала,

h –величина модального интервала,

f_Mo – частота модального интервала,

f_Mo-1 – частота интервала, предшествующего модальному,

f_Mo+1 – частота интервала, следующего за модальным.

(руб.)

Таким образом, наиболее часто встречающаяся фондоотдача среди предприятий – 1,092.

В интервальном вариационном ряду медиана рассчитывается по формуле:

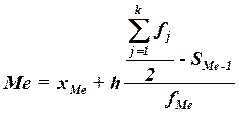
где х_Ме – нижняя граница медианного интервала,

h – величина медианного интервала,

– сумма всех частот,

f_Ме – частота медианного интервала,

S_Mе-1 – кумулятивная (накопленная) частота интервала, предшествующего медианному.

Определяем медианный интервал, в котором находится порядковый номер медианы (n).

он находится в интервале 1,060 – 1,140.

(руб.)

Таким образом, половина предприятий имеет фондоотдачу больше 1,096, а другая половина – меньше 1,096.

Чтобы рассчитать характеристики ряда распределения: среднеарифметическую, среднее квадратическое отклонение, коэффициент вариации, рассчитаем необходимые расчетные значения и результаты представим в таблице 4:

Таблица 4

Группа пред-тий по величине фондоотдачи	Число пред-тий fj	Середина интервала	Расчетное значение
1	2	3	4	5	6	7
0,900 – 0,980	3	0,940	2,82	-0,160	0,026	0,077
0,980 – 1,060	7	1,020	7,14	-0,080	0,006	0,045
1,060 – 1,140	11	1,100	12,1	0,000	0,000	0,000
1,140 – 1,220	5	1,180	5,9	0,080	0,006	0,032
1,220 – 1,300	4	1,260	5,1	0,160	0,026	0,102
Итого	30	33,00	0,064	0,256

Таблица с необходимыми расчетными значениями для расчета характеристик ряда распределения.

Средняя арифметическая определяется по формуле:

Средне квадратическое отклонение: