Реферат: Сущность и организация маркетинговой информации

N - численность генеральной (изучаемой) совокупности.

Пример. Предположим, что магазин обслуживает за определенный период около 100 000 чел. По данным предыдущих опросов установлено, что дисперсия составляет ± 25 руб./чел. Коэффициент доверия равен 2. Предельную ошибку мы приняли равной 1 руб. Тогда численность выборки составит

С округлением численность выборки составит 100 чел. Следовательно, для получения надежных представительных данных надо опросить 100 чел.

В целях повышения однородности изучаемой совокупности и большей точности расчета совокупность стратифицируют, разбивают на ряд групп по какому-то признаку. В маркетинговом исследовании наиболее распространено деление по социальным группам (в частности, по уровню дохода). Формула численности выборки отличается от предыдущей только тем, что выборочная дисперсия заменяется средней из внутригрупповых дисперсий (s-2). Однако в этом случае целесообразно вести отбор по каждой группе пропорционально дифференциации признака (n.). Тогда формула численности выборки (по каждой группе) значительно упрощается:

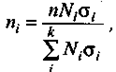(2.2)

где k — число i-х групп населения;

Ni - численность i-й группы населения;

si - среднеквадратическое отклонение признака в i-й группе.

При телефонных интервью или при анкетировании очень часто используется способ механического отбора. Например, по телефонной книге или по спискам жильцов отбирается каждый десятый телефон или каждая седьмая квартира. При использовании этого метода численность выборки определяется по формуле 3.1.

В механической выборке численность выборки определяется путем установления пропорции отбора: делением совокупности на объем выборки; если пропорция отбора дробная величина, то надо взять ближайшее целое число. Затем по списку единиц отбирается каждая единица, взятая через промежуток, равный пропорции отбора.

Пример. Для обследования, ставящего целью выявить мнение потребителей о новом товаре в регионе, насчитывающем

50 тыс. семей, необходимо провести анкетирование. Условно принимается, что в каждой квартире проживает одна семья и на нее будет выделена одна анкета. Предварительные исследования установили, что дисперсия среднего размера покупки составляет ± 25 руб.; t = 2; предельная ошибка не должна превышать 0,01 тыс. руб. Отсюда численность выборки (n) составила

Эта величина округляется до 1000 семей, т.е. установлена 2%-ная выборка. Однако практика показывает, что некоторая часть анкет не возвращается (предположим, каждая третья), поэтому увеличиваем число анкет до 500. Следовательно, необходимо включить в выборку 1500 семей, т.е. увеличить ее до 3%.

В целях ускорения процесса исследования и удешевления сбора материалов целесообразно использовать методы малой выборки. Малой выборкой считается отбор единиц численностью менее 20, т. е. n < 20.

Средняя ошибка малой выборки исчисляется по формуле

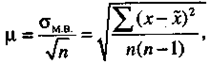(2.3)

где sмв - среднее квадратическое отклонение малой выборки, которое исчисляется по формуле:

(2.4)

где sмв - среднее квадратическое отклонение малой выборки;

s - среднее квадратическое отклонение обычной выборки;

х - независимые случайные величины (характеристики изучаемых

величин);

x̅ м.в. - средняя величина малой выборки;

n - численность выборки.

Предельная ошибка выборки определяется по следующей формуле:

(2.5)

где t - нормированное отклонение, или коэффициент доверия, который определяется по таблице вероятностей Стьюдента: