Реферат: Теоремы Ролля Коши Лагранжа Правило Лопиталя

и .

Составим теперь вспомогательную функцию, вычтя из уравнения кривой уравнение хорды:

.

Полученная функция непрерывна на отрезке и дифференцируема во всех его внутренних точках. Кроме того, вычисление в точках и показывает, что . Значит, функция на отрезке удовлетворяет требованиям теоремы Ролля. Но в этом случае существует такая точка , в которой .

Вычислим производную функции :

.

Согласно теореме Ролля в точке производная , то есть и

,

что и требовалось доказать.

Геометрический смысл теоремы Лагранжа следующий: внутри отрезка существует, по крайней мере, одна точка, в которой касательная параллельна хорде, стягивающей кривую на данном отрезке. В частности, при теорема переходит в теорему Ролля.

Теорему Лагранжа часто записывают в следующем виде:

,

то есть приращение функции равно приращению аргумента, умноженному на производную функции в некоторой внутренней точке. В связи с этим теорему Лагранжа называют также теоремой о конечных приращениях.

3. Теорема Коши

Рассмотрим, наконец, третью теорему о среднем, принадлежащей Коши (1789–1859), которая является обобщением теоремы Лагранжа.

Теорема. Если функции и непрерывны на отрезке и дифференцируемы во всех его внутренних точках, причем не обращается в ноль ни в одной из указанных точек, то существует, по крайней мере, одна точка , в которой .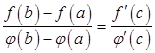

Доказательство. Так как во всех точках , то отсюда следует, что . В противном случае, как следует из теоремы Ролля, существовала хотя бы одна точка , в которой .

Составим вспомогательную функцию

.

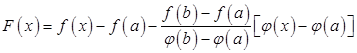Данная функция непрерывна на отрезке и дифференцируема во всех его внутренних точках. Кроме того, вычисление ее в точках и дает: . Значит, функция удовлетворяет требованиям теоремы Ролля, то есть существует хотя бы одна точка , в которой .

Вычислим производную :

.

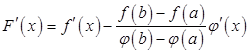Из условия следует, что

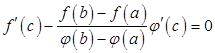и ,

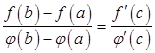что и требовалось доказать.

В случае, когда , теорема Коши переходит в формулировку теоремы Лагранжа.

4. Правило Лопиталя

На основании теоремы Коши о среднем можно получить удобный метод вычисления некоторых пределов, называемый правилом Лопиталя (1661–1704).

Теорема. Пусть функции и непрерывны и дифференцируемы во всех точках полуинтервала и при совместно стремятся к нулю или бесконечности. Тогда, если отношение их производных имеет предел при , то этот же предел имеет отношение и самих функций, то есть 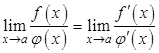.