Реферат: Теоремы Ролля Коши Лагранжа Правило Лопиталя

Возьмем точку . Так как функции и удовлетворяют теореме Коши (п. 2.14), применим ее на отрезке :

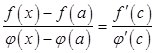, где .

Так как , то

.

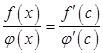Перейдем в данном равенстве к пределу:

.

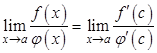Но если , то и , находящееся между точками и , будет стремится к , значит

.

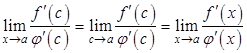Отсюда, если 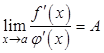, то и 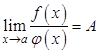, то есть

,

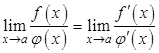что и требовалось доказать.

Если при , то снова получается неопределенность вида и правило Лопиталя можно применять снова, то есть

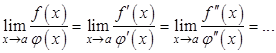
Доказательство правила Лопиталя для случая проводится сложнее, и мы его рассматривать не будем.

При раскрытии неопределенностей типа , , , , правило Лопиталя применять непосредственно нельзя. Вначале все эти неопределенности необходимо преобразовать к виду или .

Правило Лопиталя может быть использовано при сравнении роста функций, в случае когда . Наибольший практический интерес здесь представляют функции , , . Для этого найдем пределы их отношений:

1) , значит, растет быстрее, чем ;

2) , значит, растет быстрее, чем ;

3) , значит, растет быстрее, чем .

Отсюда следует, что быстрее всего растет , затем и, наконец, .

Литература

1. Гмурман В.Е. Теория вероятностей и математическая статистика. М., «Высшая школа» изд. 5, 1977.

2. Зайцев И.А. Высшая математика. ДРОФА, 2005. – 400 с.

3. Краснов М. Вся высшая математика т. 1 изд. 2. Едиториал УРСС, 2003. – 328 с.

4. Краснов М.Л., Макаренко Г.И., Киселев А.И., Шикин Е.В. Вся высшая математика Интегральное исчисление. Дифференциальное исчисление функций нескольких переменных. Дифференциальная геометрия Том 2.: Учебник – 3-е изд. ЛКИ, 2007.

5. Мироненко Е.С. Высшая математика. М: Высшая школа, 2002. – 109 с.