Реферат: Теория гидродинамической смазки в гидравлике
l – слой смазочного материала, 2 – цапфа, 3 – подшипник, r – радиус цапфы, u – окружная скорость цапфы, δ – толщина зазора, λ- эксцентриситет
Для краткого ознакомления с теорией смазки рассмотрим трение цапфы радиусом r и длиной l в подшипнике при ее концентричном вращении (рис.1, а).
Предположим, что слой смазочного материала, покрывающий цапфу, имеет одинаковую толщину δ. При вращении цапфы с окружной скоростью uчастицы смазочного материала на поверхности цапфы будут иметь ту же скорость. По мере удаления от цапфы эта скорость будет уменьшаться и на поверхности подшипника станет равной нулю.
Сила трения между цапфой и смазочным материалом
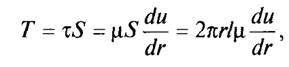
где ![]() - площадь поверхности цапфы.
- площадь поверхности цапфы.
Приняв, что скорость вращения частиц смазочного материала на толщине слоя δ линейно изменяется от u до нуля, можно определить градиент скорости как du/dr = u/δ. Тогда
![]()
Н.П. Петров получил более точное выражение для силы трения цапфы

Где λ – коэффициенты трения для внутреннего и внешнего цилиндров.
Сила трения прямо пропорциональна вязкости жидкости и числу оборотов и обратно пропорциональна толщине смазывающего слоя.
Предложенная Н.П. Петровым гидродинамическая теория смазки в дальнейшем была развита Н.Е. Жуковским и C.А. Чаплыгиным в труде «О трении смазочного слоя между шипом и подшипником»
3 Трение смазочного слоя между шипом и подшипником
Движение вязкой жидкости, заключенной в смазочном слое между шипом и подшипником, было сначала исследовано Н.П. Петровым, который положил основание гидродинамической теории шипа. Н.П. Петров принимал смазочный слой ограниченный двумя концентрическими цилиндрами. Влияние на рассматриваемое явление эксцентричности шипа и подшипника было с помощью приближенного анализа обстоятельно исследовано Осборном Рейнольдсом. Довольно сложный анализ был упрощен Зоммерфельдом, который установил теоретическую зависимость между моментом сил трения, нагрузкою и скоростью шипа и показал, пропорциональность момента сил трения его скорости или его нагрузки суть два предельные случая общего закона трения шипа и подшипника, причем первый предельный случай получается при больших, а второй при малых скоростях шипа. Точное решение задачи о движении вязкой жидкости в двух измерениях между двумя эксцентрическими окружностями, равно как решение аналитической задачи о равновесии упругой пластины, ограниченной двумя эксцентрическими окружностями, до сих пор ещё не найдено.
Заключение
Расчет подшипников на основании гидродинамической теории смазки раскрывает многие стороны работы подшипников недоступные расчету на основе средних удельных давлений. Для дальнейшего совершенствования подшипников автомобильных двигателей абсолютно необходимо вести их расчет методом гидродинамической теории. Применение данной методики определения движения шейки коренного подшипника невозможно без дальнейшей доработки.
Список используемой литературы
1. Гидравлика, гидромашины и гидропневмопривод: учеб. Пособие для студ. Высшее учеб. Заведение [Т.В. Артемьева, А.Н. Румянцева, С.П. Стесин]; под ред. С.П. Стесина – 4-е изд., М.: Издательский центр «Академия», 2008. – 336 с.
2. Ухин Б.В., Гусев А.А. Гидравлика: Учебник. – М.: ИНФРА – М, 2008, - 432 с – (среднее профессиональное образование)
3. Машиностроительная гидравлика. Башта Т.М., «Машиностроение», 1971, 672 с.