Реферат: Теория Матриц и Определителей

Оглавление......................................................................................................................................................

1. Матрицы.........................................................................................................................................................

1.1 Понятие матрицы....................................................................................................................................

1.2 Оновные операции над матрицами................................................................................................

2. Определители...........................................................................................................................................

2.1 Понятие определителя..........................................................................................................................

2.2 Вычисление определителей................................................................................................................

2.3 Основные свойства определителей................................................................................................

3. Системы линейных уравнений................................................................................................

3.1 Основные определения.........................................................................................................................

3.2 Условие совместности систем линейных уравнений...........................................................

3.3 Решение ситем линейных уравнений метедом Крамера.....................................................

3.4 Решение ситем линейных уравнений метедом Гаусса........................................................

4. Обратная матрица.................................................................................................................................

4.1 Понятие обратной матрицы................................................................................................................

4.2 Вычесление обратной матрицы........................................................................................................

Список литературы..................................................................................................................................

1. Матрицы.

1.1 Понятие матрицы.

Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество n столбцов. Числа m и n называются порядками матрицы. В случае, если m = n , матрица называется квадратной, а число m = n -- ее порядком .

1.2 Основные операции над матрицами.

Основными арифметическими операциями над матрицами являются умножение матрицы на число, сложение и умножение матриц.

Прежде всего договоримся считать матрицы равными, если эти матрицы имеют одинаковые порядки и все их соответствующие элементы совпадают.

Перейдем к определению основных операций над матрицами.

Сложение матриц : Суммой двух матриц, например: A и B , имеющих одинаковое количество строк и столбцов, иными словами, одних и тех же порядков m и n называется матрица С = ( С ij )( i = 1, 2, …m; j = 1, 2, …n ) тех же порядков m и n , элементы Cij которой равны.

Cij = Aij + Bij ( i = 1, 2, …, m; j = 1, 2, …, n ) ( 1.2 )

Для обозначения суммы двух матриц используется запись C = A + B. Операция составления суммы матриц называется их сложением

Итак по определению имеем :

+ =

=

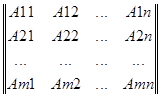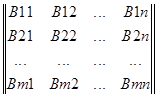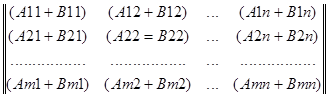
Из определения суммы матриц, а точнее из формулы ( 1.2 ) непосредственно вытекает, что операция сложения матриц обладает теми же свойствами, что и операция сложения вещественных чисел, а именно :

1) переместительным свойством : A + B = B + A

--> ЧИТАТЬ ПОЛНОСТЬЮ <--