Реферат: Теория общего равновесия и относительные цены в России на современном этапе
Пусть избыточный спрос (предложение) i-го субъекта
на рынке А - Δ Аi = Adi - Аsi;
на рынке В - Δ Bi = Bdi - Bsi;
на рынке C - Δ Ci = Cdi - Csi;
на рынке N - Δ Ni = Ndi - Nsi;
PA, PB, PC :. PN - соответственно цены товаров A, B, C : N.
Суммарный результат сделок i-го субъекта можно выразить формулой
PA Δ Ai + PB ΔBi + PC ΔCi +:. + PN ΔNi = 0 (2.1.2)
Просуммируем избыточный спрос всех участников рыночных сделок на каждом из N рынков:
(2.1.3)
Если существует одновременное равновесие на N-1 рынках, то:
∑ΔAi + ∑Δ Bi + ∑Δ Ci + : + ∑Δ (N-1)i = 0 ( 2.1.4),
но в таком случае уравнение (2.1.3) соблюдается при ∑Δ Ni = 0 , так как РN не равно нулю. Это означает, что закон Вальраса доказан.
2.2.Практическая часть.
Для упрощения возьмем экономику без производства (меновое хозяйство; стадия производства завершена и произведенные объемы благ обмениваются на рынках). Хозяйство состоит из трех индивидов, потребляющих три вида благ A, B и H. В исходном состоянии первый потребитель имеет QA0 , второй - QB0 и третий - QH0 ед. указанного блага. Поэтому индивиды совершают обмен при следующих бюджетных ограничениях:
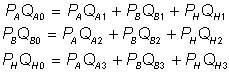
Известны функции полезности каждого потребителя
где Qij - объем потребления j-го блага (j = A, B, H) i-м индивидом.
Функции спроса потребителей на каждое из благ выводятся из максимизации функции полезности при заданном бюджетном ограничении; используем для этого функцию Лагранжа.
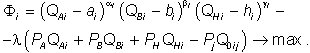
Условия ее максимизации
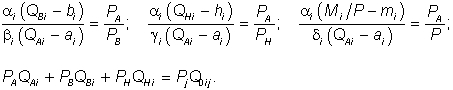
Из них выводятся следующие функции спроса:
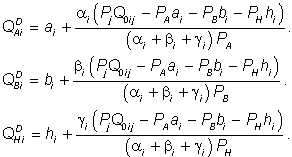
Система цен, обеспечивающая общее экономическое равновесие, должна приравнять объемы спроса на блага имеющимся запасам
В соответствии с законом Вальраса только два из этих трех уравнений являются независимыми. Приняв цену одного из благ за 1, уменьшаем число неизвестных до числа независимых уравнений и из решения системы двух уравнений определяется вектор относительных (реальных) равновесных цен (
). Для определения уровня цен (Р) и вектора денежных (номинальных) цен используется уравнение количественной теории денег:
Пример. Функции полезности потребителей имеют вид