Реферат: Теория структурообразования
На графике есть три участка:
1) 0 < h < h 1 •U (h) < 0, между частицами преобладают силы притяжения, наблюдается ближний минимум.
U отт → const; U пр → -∞. Происходит коагуляция.
2) h 1 < h < h 2 . U (h ) > 0 – между частицами преобладают силы отталкивания. U отт > |U пр |.
3) h 2 < h < h 3 . U (h ) < 0 – обнаруживается дальний минимум, однако глубина его невелика.
При h = h 1 , h 2 , h 3 U (h ) = 0, т. е. при этих расстояниях между частицами силы притяжения уравновешиваются силами отталкивания.
Таким образом, если частицы сблизятся на расстояние меньше h 1 , они неизбежно слипнутся, но для этого должен быть преодолён потенциальный барьер ∆ U к . Это возможно при достаточной кинетической энергии частиц, которая среднестатистически близка к произведению κТ .
Рассмотрим взаимодействие двух частиц. Будем одну частицу считать неподвижной, а вторую – приближающейся к ней с энергией, равной κТ .
Если κТ < ∆ Umin , частицы останутся на расстоянии hmin и будут связаны между собой через слой дисперсионной среды, т. е. образуют “пару”, но непосредственно не слипаются и не теряют своей седиментационной устойчивости. В таких случаях говорят, что взаимодействие происходит в дальнем минимуме.
Если ∆Umin < κ Т << ∆U к , то частицы при столкновении отлетают друг от друга. Система агрегативно устойчива.
Если κТ < ∆ U к , то происходит медленная коагуляция.
Если κТ > ∆ U к , то происходит быстрая коагуляция.
Так как золь обычно рассматривают при постоянной температуре, кинетическая энергия частиц остаётся постоянной. Следовательно, для коагуляции должен быть уменьшен потенциальный барьер коагуляции ∆ U к .
Обычно для понижения потенциального барьера в систему вводится электролит-коагулянт. Теория ДЛФО даёт возможность вычислить порог быстрой коагуляции СКБ :
![]() ,
,
где А , В – постоянные величины, которые могут быть рассчитаны;
ε – диэлектрическая проницаемость среды;
Z – заряд иона-коагулянта;
ē – заряд электрона.
Из этой формулы видно, что зависимость порога коагуляции от заряда иона-коагулянта, выведенная из теории ДЛФО, согласуется с эмпирическим правилом Шульце-Гарди:
![]() .
.
Жидкообразные и твердообразные тела. Ньютоновские и неньютовские жидкости. Псевдопластические и дилатантные жидкообразные тела. Уравнение Оствальда-Вейля. Бингамовские и небингамовские твердообразные тела. Тиксотропия и реопексия
Предложенная П.А. Ребиндером классификация структур дисперсных систем помогает связать механические свойства тел с их строением.
В соответствии с реологическими свойствами все реальные тела делят на жидкообразные (предел текучести равен нулю, РТ = 0) и твердообразные (РТ > 0).
Жидкообразные тела классифицируют на ньютоновские и неньютоновские жидкости . Ньютоновские жидкости – это системы, вязкость которых не зависит от напряжения сдвига и является постоянной величиной в соответствии с законом Ньютона. Течение неньютоновских жидкостей не следует закону Ньютона, их вязкость зависит от напряжения сдвига. Неньютоновские жидкости подразделяются на стационарные , реологические свойства которых не меняются во времени, и нестационарные , для которых эти характеристики зависят от времени. Неньютоновские стационарные жидкости подразделяются на псевдопластические и дилатантные (рис. 4.1.2.1 и 4.1.2.2).
Исходя из экспериментальных исследований, графические зависимости напряжения сдвига от скорости деформации в логарифмических координатах часто линейны и различаются только тангенсом угла наклона прямой, поэтому общую зависимость напряжения сдвига Р от скорости деформации g можно выразить в виде степенной функции:
![]() ,
,
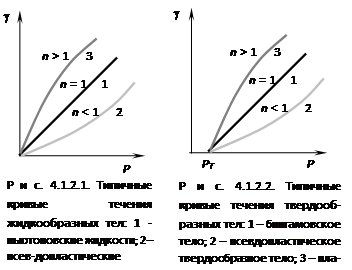 где k иn – постоянные, характеризующие данную жидкообразную систему.
где k иn – постоянные, характеризующие данную жидкообразную систему.
Двухпараметрическое уравнение – математическая модель Оствальда-Вейля : ньютоновская вязкость h неньютоновской стационарной жидкости определяется уравнением