Реферат: Тестирование и верификация HDL-моделей компонентов SOC

module Xilinx

`timescale 1ns/10ps

module dct ( CLK, RST, xin,dct_2d,rdy_out);

output [11:0] dct_2d;

input CLK, RST;

input[7:0] xin; /* input */

output rdy_out;

wire[11:0] dct_2d;

………………….

/* The first 1D-DCT output becomes valid after 14 +64 clk cycles. For the first 2D-DCT output to be valid it takes 78 + 1clk to write into the ram + 1clk to write out of the ram + 8 clks to shift in the 1D-DCT values + 1clk to register the 1D-DCT values + 1clk to add/sub + 1clk to take compliment + 1 clk for multiplying + 2clks to add product. So the 2D-DCT output will be valid at the 94th clk. rdy_out goes high at 93rd clk so that the first data is valid for the next block*/

Endmodule

В соответствии с правилами тестопригодного анализа, приведенными выше, спроектирован транзакционный граф как развитие графа регистровых передач, представленный на рис. 4, который для module Xilinx имеет 28 вершин-компонентов (входная и выходная шины, логические и регистровые переменные, векторы и память).

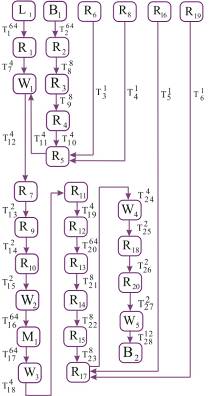
Рис. 4. Транзакционный граф Xilinx модели

Идентификатор дуги имеет верхний индекс, обозначающий число транзакций в программе между исходящей и входящей вершинами. Для каждой вершины строятся логические функции управляемости и наблюдаемости. Пример логической функции управляемости для вершины имеет следующий вид:

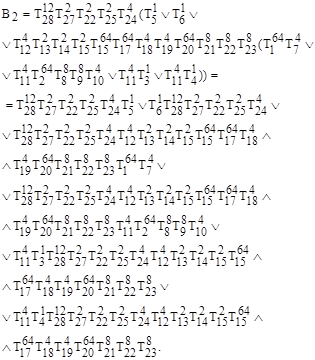
Для остальных вершин аналогично выполняется вычисление ДНФ функций управляемостей.

Примеры вычисления функций наблюдаемостей для отдельных вершин имеют следующий вид:

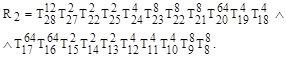
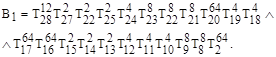
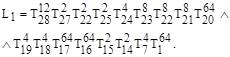
Синтезированные логические функции задают все возможные пути управления, как во времени, так и в пространстве, что можно считать новой аналитической формой описания тестопригодности проекта. По ДНФ, следуя выражениям для подсчета тестопригодности, можно определить критерии управляемости (наблюдаемости) для всех компонентов HDL-модели. Здесь следует рассмотреть для варианта (сценария) обсчета программной модели. 1) Учитывается только графовая структура, где вес каждой дуги равен 1, независимо от числа транзакций в программном коде. 2). Все дуги графа отмечаются реальным количеством транзакций, имеющих место быть между двумя рассматриваемыми вершинами-компонентами транзакционного графа. Оценки тестопригодности описанных процедур могут существенно различаться друг от друга. Пользователь должен определиться, что важнее только структура программного кода – применить первый сценарий, или иметь более сложную и точную модель транзакций, распределенных во времени, на множестве графовых компонентов. В качестве примера ниже приводится процедура вычисления управляемости для вершины :

.

Применение аналогичных вычислений управляемостей (наблюдаемостей) для других вершин графа дает результат в виде графика, представленного на рис. 5, которые позволяют определить критические точки для установки необходимых ассерций.

Такой вершиной может быть компонент , если транзакционный граф представлен одиночными дугами. Для случая, когда дуги отмечены реальным количеством транзакций, критические вершины принадлежат компонентам, находящихся ближе к выходной шине . Здесь существенным представляется не структура графа, а вес дуги входящей, который в большей степени оказывает негативное влияние, если структурная глубина рассматриваемого компонента достаточно высока. Используется формула (1) вычисления тестопригодности с мультипликативными членами , что дает оценку ниже, чем любой из сомножителей (управляемость, наблюдаемость).

Если модифицировать формулу (1) исчисления тестопригодности для компонентов к следующему виду:

,

то кривая тестопригодности существенно поднимется вверх по оси ординат, чем обеспечивается меньший разброс параметров для каждой вершины. Данное обстоятельство фиксирует несколько отличные таблицы и графики, представленные ниже (рис.6).