Реферат: Тестирование и верификация HDL-моделей компонентов SOC

Рис. 5. Графики М-тестопригодности Xilinx модели

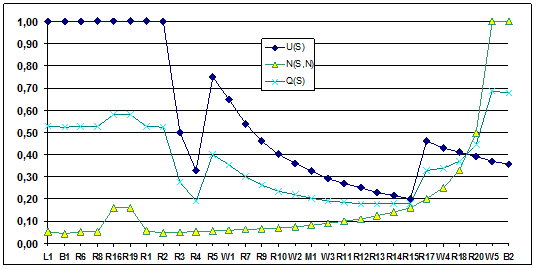
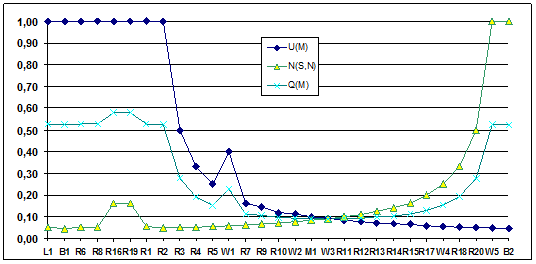
Рис. 6. Графики A-тестопригодности Xilinx модели

Интересным представляется поведение отдельных вершин. Например, управляемость вершины в мультипликативном транзакционном графе HDL-кода неожиданно «упала» вниз по сравнению с графом единичных дуг. Это связано с высоким весом транзакций, поступающих на рассматриваемую вершину со стороны входных компонентов , которые практически превращают в ноль значимость единичных транзакций от вершин .

После определения управляемостей и наблюдаемостей вершин транзакционного графа выполняется подсчет обобщенного критерия тестопригодностей каждого компонента программного кода в соответствии с выражением (5). Затем определяется интегральная оценка тестопригодности проекта по формуле:

,

которая определяет качество проектного варианта, что представляется весьма существенным при сравнении нескольких альтернативных решений. В качестве примера позитивного использования разработанных моделей и методов предлагается анализ тестопригодности программного кода дискретного косинусного преобразования из Xilinx библиотеки. Было выполнено построение транзакционной модели, подсчет характеристик тестопригодности (), определение критических точек. Затем в соответствии с числом и типами компонентов было разработано функциональное покрытие, фрагмент которого представлен листингом 2.

Листинг 2.

c0: coverpoint xin

{

bins minus_big={[128:235]};

bins minus_sm={[236:255]};

bins plus_big={[21:127]};

bins plus_sm={[1:20]};

bins zero={0};

}

c1: coverpoint dct_2d

{

bins minus_big={[128:235]};

bins minus_sm={[236:255]};

bins plus_big={[21:127]};

bins plus_sm={[1:20]};

bins zero={0};

bins zero2=(0=>0);

}

endgroup

Для критических точек, определенных в результате анализа тестопригодности транзакционного графа разработана ассерционная модель проверки основных характеристик дискретного косинусного преобразования. Существенный фрагмент кода механизма ассерций представлен листингом 3.

Листинг 3.