Реферат: Типовой расчет по ЭМММ
Выполнил:
Проверил:
Екатеринбург
2009
Математическая модель ЗЛП
Мат. модель ЗЛП называется стандартной, если система ограничений представлена в виде неравенств, а функция минимизируется или максимизируется
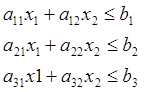
- система ограничений
- целевая функция
X=(x1,x2) – основное (оптимальное) решение
![]() (>= в системе ограничений min )
(>= в системе ограничений min )
Целевая f(x) является линейной, поэтому частные производные отличны от нуля, т к является const, следовательно экстремальных значений внутри области ограничений нет. Если функция имеет оптимальное значение, то оно достигается на границах области.
Задача:
Предприятие выпускает 2 вида продукции А1 и А2, использую при этом 3 вида сырья S1, S2, S3. Известны запасы сырья- b1, b2, b3. Расход сырья вида Si на производство продукции Aj=aij.Доход от реализации одной единицы продукции Aj составляет Сj у.е.
Требуется составить такой план производства продукции, при котором доход будет максимален.
Решить задачу графическим методом; составить каноническую модель задачи и решить её симплекс методом; Найти двойственные оценки цен на сырье из решения симметричной двойственной задачи по теоремам двойственности.
|
Сырье |
А1 |
А2 |
bi |
|
S1 | 5 | 2 | 40 |
|
S2 | 1 | 3 | 30 |
|
S3 | 4 | 3 | 39 |
|
Cj | 2 | 3 |
Решение задачи графическим методом
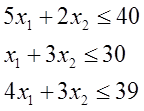 |
![]() f(X) = 2x + 3x max
f(X) = 2x + 3x max
L1: 5х + 2х = 40 | : 40
x / 8 + x / 20 = 1
L2 : x + 3x =30 | : 30
x / 30 + x / 10 = 1
L3 : 4х + 3х = 39
|
| 0 | 9,75 |
|
Х | 13 | 0 |
--> ЧИТАТЬ ПОЛНОСТЬЮ <--