Реферат: Точные методы решения систем линейных алгебраических уравнений (СЛАУ)

Реферат

на тему:

Точные методы решения систем линейных алгебраических уравнений (СЛАУ)

Введение

Данная лабораторная работа включает в себя два точных метода решения систем линейных алгебраических уравнений (СЛАУ):

Метод Гаусса.

Метод Холецкого.

Также данная лабораторная работа включает в себя: описание метода, применение метода к конкретной задаче (анализ), код программы решения вышеперечисленных методов на языке программирования Borland C++ Builder 6.

Описание метода:

Метод решения СЛАУ называют точным (прямым), если он позволяет получить решение после выполнения конечного числа элементарных операций. К прямым методам относят метод Крамера, метод Гаусса, метод Холецкого и другие. Основным недостатком прямых методов является то, что для нахождения решения необходимо выполнить большое число операций.

Сначала рассмотрим наиболее распространённый метод решения СЛАУ - метод Гаусса, состоящий в последовательном исключении неизвестных.

Пусть дана система уравнений

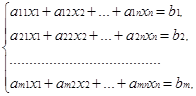(1)

Процесс решения по методу Гаусса состоит из двух этапов. На первом этапе (прямой ход) система приводится к ступенчатому виду:

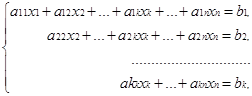
где kn, aii 0, i=, аii - главный элемент системы.

На втором этапе (обратный ход) идет последовательное определение неизвестных из этой ступенчатой системы.

Прямой ход.

Положим а11 0, если а11 = 0, то первым в системе запишем уравнение, в котором а11 0.

Расставим уравнения системы таким образом, чтобы коэффициент при х1 имел наибольшее значение (другими словами отсортируем систему по убыванию).

Преобразуем систему, исключив неизвестное х1 во всех уравнениях, кроме первого (используя элементарные преобразования системы). Для этого умножим обе части первого уравнения на и сложим почленно со вторым уравнением системы. Затем умножим обе части первого уравнения на и сложим с третьим уравнением системы. Продолжая этот процесс, получаем систему

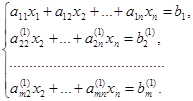
Здесь (i, j = ) - новые значения коэффициентов и правых частей, которые получаются после первого шага.

--> ЧИТАТЬ ПОЛНОСТЬЮ <--