Реферат: Три кризиса в развитии математики
Ïî ïîâîäó ýòîãî îòêðûòèÿ Àðèñòîòåëü ãîâîðèë, ÷òî Ïèôàãîð ïîêàçàë, ÷òî åñëè áû äèàãîíàëü êâàäðàòà áûëà áû ñîèçìåðèìà ñ åãî ñòîðîíîé, òî ÷åòíîå ðàâíÿëîñü áû íå÷åòíîìó.
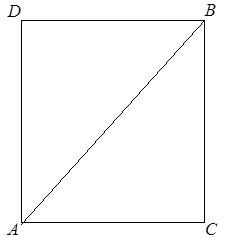 Ðèñ. 1 Ðèñ. 1 |
Ýòî çàìå÷àíèå Àðèñòîòåëÿ ÿñíî ïîêàçûâàåò, ÷òî ïðè äîêàçàòåëüñòâå íåñîèçìåðèìîñòè äèàãîíàëè êâàäðàòà ñ åãî ñòîðîíîé Ïèôàãîð èñïîëüçîâàë ìåòîä îò ïðîòèâíîãî (ðèñ. 1).
Ïóñòü, äåéñòâèòåëüíî, äèàãîíàëü ÀÂ ñîèçìåðèìà ñî ñòîðîíîé ÀÑ êâàäðàòà ÀÑÂÄ .
Òîãäà 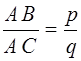 , ãäå ð è q — íàòóðàëüíûå ÷èñëà. Äðîáü
, ãäå ð è q — íàòóðàëüíûå ÷èñëà. Äðîáü ![]() ìîæíî ñ÷èòàòü íåñîêðàòèìîé (èíà÷å å¸ ìîæíî áûëî áû ñîêðàòèòü); çíà÷èò, ð èëè q áóäåò ÷èñëîì íå÷åòíûì.
ìîæíî ñ÷èòàòü íåñîêðàòèìîé (èíà÷å å¸ ìîæíî áûëî áû ñîêðàòèòü); çíà÷èò, ð èëè q áóäåò ÷èñëîì íå÷åòíûì.
Ïðèìåì ÀÑ =1. Ïî òåîðåìå Ïèôàãîðà äîëæíî áûòü:
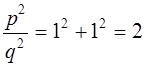 ;
;
Çíà÷èò
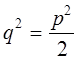 ,
,
ò. å. ð 2 äåëèòñÿ íàöåëî íà 2; ñëåäîâàòåëüíî è ð òàêæå äåëèòñÿ íàöåëî íà 2:
ð=2ð 1 ,
ãäå ð 1 — íåêîòîðîå íàòóðàëüíîå ÷èñëî.
Àíàëîãè÷íî ïîëó÷àåì:
q=2q 1 ,
ãäå q 1 òàêæå íåêîòîðîå íàòóðàëüíîå ÷èñëî.
Èòàê, ð è q — îáà ÷åòíûå ÷èñëà. Ïîñêîëüêó ð èëè q — ÷èñëî íå÷åòíîå, âûõîäèò, ÷òî ÷åòíîå ÷èñëî ðàâíî íå÷åòíîìó ÷èñëó.  êîíöå V âåêà äî í. ý. Ôåîäîð èç Êèðåíû óñòàíîâèë, ÷òî íåñîèçìåðèìîñòü äèàãîíàëè êâàäðàòà ñ åãî ñòîðîíîé íå ÿâëÿåòñÿ èñêëþ÷åíèåì. Îí ïîêàçàë, ÷òî ñòîðîíû êâàäðàòîâ, ïëîùàäè êîòîðûõ ðàâíû 3, 5, 6, …, 17 íåñîèçìåðèìû ñî ñòîðîíîé åäèíè÷íîãî êâàäðàòà. Ïèôàãîð ó÷èë, ÷òî ñóùíîñòü âñåõ âåùåé åñòü ÷èñëî; ÷èñëî — ñàìè âåùè; ãàðìîíèÿ ÷èñåë — ãàðìîíèÿ ñàìèõ âåùåé. Àðèñòîòåëü ãîâîðèë, ÷òî ó ïèôàãîðåéöåâ ÷èñëà ïðèíèìàëèñü çà íà÷àëî è â êà÷åñòâå ìàòåðèè è â êà÷åñòâå [âûðàæåíèÿ äëÿ] èõ ñîñòîÿíèÿ è ñâîéñòâ.
Îòêðûòèå íåñîèçìåðèìûõ âåëè÷èí ñíà÷àëà “âûçâàëî óäèâëåíèå” (Àðèñòîòåëü). Ýòî åñòåñòâåííî: äî îòêðûòèÿ Ïèôàãîðà äðåâíåãðå÷åñêèå ìàòåìàòèêè ñ÷èòàëè, ÷òî ëþáûå äâà îòðåçêà èìåþò îáùóþ ìåðó, õîòÿ, ìîæåò áûòü, è î÷åíü ìàëóþ. Êîãäà, îäíàêî, ïèôàãîðåéöû óáåäèëèñü, ÷òî äîêàçàòåëüñòâî ñóùåñòâîâàíèÿ íåñîèçìåðèìûõ âåëè÷èí áåçóïðå÷íî, îíè ïîíÿëè, ÷òî èõ ôèëîñîôèÿ îêàçàëàñü â çàòðóäíèòåëüíîì ïîëîæåíèè.
Ïèôàãîðåéöû çíàëè òîëüêî ïîëîæèòåëüíûå öåëûå è äðîáíûå ÷èñëà. Ñëåäóÿ ñâîåé ôèëîñîôñêîé óñòàíîâêå, îíè, ïî ñóòè äåëà, ñ÷èòàëè, ÷òî êàæäàÿ âåùü ìîæåò áûòü îõàðàêòåðèçîâàíà ïîëîæèòåëüíûì öåëûì èëè äðîáíûì ÷èñëîì, êîòîðîå “âûðàæàåò ñóùíîñòü” ýòîé âåùè. Íà äåëå ýòî îçíà÷àëî, ÷òî ãåîìåòðèÿ ñòðîèëàñü íà áàçå àðèôìåòèêè. Îòêðûòèå íåñîèçìåðèìûõ îòðåçêîâ çíàìåíîâàëî ïîýòîìó íà÷àëî êðèçèñà ïèôàãîðåéñêîé ôèëîñîôèè è ìåòîäîëîãè÷åñêèõ îñíîâ ðàçâèâàåìîé èìè ñèñòåìû ìàòåìàòèêè. Ïîñëå îáíàðóæåíèÿ ñóùåñòâîâàíèÿ íåñîèçìåðèìûõ âåëè÷èí ïåðåä ïèôàãîðåéöàìè îòêðûëèñü äâå âîçìîæíîñòè. Ìîæíî áûëî ïîïûòàòüñÿ ðàñøèðèòü ïîíÿòèå ÷èñëà çà ñ÷åò ïðèñîåäèíåíèÿ ê ðàöèîíàëüíûì ÷èñëàì ÷èñåë èððàöèîíàëüíûõ, îõàðàêòåðèçîâàòü íåñîèçìåðèìûå âåëè÷èíû ÷èñëàìè èíîé ïðèðîäû è òàêèì îáðàçîì âîññòàíîâèòü ñèëó ôèëîñîôñêîãî ïðèíöèïà “âñå åñòü ÷èñëî”.
Îäíàêî, ýòîò ïóòü ñòîëü åñòåñòâåííûé è ïðîñòîé ñ ñîâðåìåííîé òî÷êè çðåíèÿ, äëÿ ïèôàãîðåéöåâ áûë çàêðûò.  ýòîì ñëó÷àå íàäî áûëî ïîñòðîèòü äîñòàòî÷íî ñòðîãóþ àðèôìåòè÷åñêóþ òåîðèþ äåéñòâèòåëüíûõ ÷èñåë, ÷òî ïðè óðîâíå ïèôàãîðåéñêîé ìàòåìàòèêè áûëî äåëîì íåâûïîëíèìûì. Ïîýòîìó íàäî áûëî èäòè ïî äðóãîìó ïóòè — ïî ïóòè îïðåäåëåííîãî ïåðåñìîòðà èñõîäíûõ ïðèíöèïîâ, íàïðèìåð ïðèíÿòü, ÷òî ãåîìåòðè÷åñêèå îáúåêòû ÿâëÿþòñÿ âåëè÷èíàìè áîëåå îáùåé ïðèðîäû, ÷åì äðîáíûå è öåëûå ÷èñëà, è ïûòàòüñÿ ñòðîèòü âñþ ìàòåìàòèêó íå íà àðèôìåòè÷åñêîé, à íà ãåîìåòðè÷åñêîé îñíîâå. Èìåííî ýòîò âòîðîé ïóòü è èçáðàëè ïèôàãîðåéöû, à âñëåä çà íèìè áîëüøèíñòâî äðåâíåãðå÷åñêèõ ìàòåìàòèêîâ, âïëîòü äî Àðõèìåäà è Àïîëëîíèÿ.
2. Проблема бесконечности в
древнегреческой философии и математике
 äðåâíåãðå÷åñêîé ôèëîñîôèè ïîíÿòèå áåñêîíå÷íîñòè ïîÿâèëîñü âïåðâûå ó ìàòåðèàëèñòîâ ìèëåòñêîé øêîëû. Àíàêñèìàíäð (610–546 ãã. äî í. ý.), ïåðååìíèê Ôàëåñà, ó÷èë: ìàòåðèÿ áåñêîíå÷íà â ïðîñòðàíñòâå è âî âðåìåíè; âñåëåííàÿ áåñêîíå÷íà, ÷èñëî ìèðîâ áåñêîíå÷íî. Àíàêñèìåí (546 ã. äî í. ý. — ðàñöâåò äåÿòåëüíîñòè) ãîâîðèë: âå÷íûé êðóãîâîðîò ìàòåðèè — ýòî è åñòü áåñêîíå÷íîñòü.
Ïîíÿòèå áåñêîíå÷íîñòè êàê ìàòåìàòè÷åñêàÿ êàòåãîðèÿ âïåðâûå ïîÿâëÿåòñÿ ó Àíàêñèãîðà (îêîëî 500–428 ãã. äî í. ý.).  ñî÷èíåíèè “Î ïðèðîäå” Àíàêñèãîð ïèñàë: âåùè áåñêîíå÷íî äåëèìû, íåò ïîñëåäíåé ñòóïåíè äåëèìîñòè ìàòåðèè; ñ äðóãîé ñòîðîíû, âñåãäà èìååòñÿ íå÷òî áîëüøåå, ÷òî ÿâëÿåòñÿ áîëüøèì.
Áåñêîíå÷íîñòü äëÿ Àíàêñîãîðà — ïîòåíöèàëüíàÿ; îíà ñóùåñòâóåò â äâóõ ôîðìàõ: êàê áåñêîíå÷íî ìàëîå è áåñêîíå÷íî áîëüøîå.  ìàòåìàòèêå òî÷êà çðåíèÿ Àíàêñàãîðà íàøëà áëàãîïðèÿòíóþ ïî÷âó áëàãîäàðÿ îòêðûòèþ íåñîèçìåðèìûõ âåëè÷èí — âåëè÷èí, êîòîðûå íå ìîãóò áûòü èçìåðåíû ëþáîé, êàêîé óãîäíî ìàëîé, îáùåé ìåðîé.
Äåìîêðèò (îêîëî 560–570 ãã. äî í. ý.), ïî-âèäèìîìó, èçó÷àë òàê íàçûâàåìûå ðîãîâèäíûå óãëû (óãëû, îáðàçóåìûå äóãîé îêðóæíîñòè è êàñàòåëüíîé ê íåé).
Ïîñêîëüêó êàæäûé ðîãîâèäíûé óãîë “ìåíüøå” ëþáîãî ïðÿìîëèíåéíîãî óãëà, çäåñü ïîÿâëÿåòñÿ ïîíÿòèå àêòóàëüíî áåñêîíå÷íî ìàëîãî. Âïîñëåäñòâèè ïîÿâèëîñü è ïîíÿòèå àêòóàëüíîé áåñêîíå÷íîñòè.
Àðèñòîòåëü (384–322 ãã. äî í. ý.) îò÷åòëèâî ðàçëè÷àåò äâà âèäà áåñêîíå÷íîñòè: ïîòåíöèàëüíóþ è àêòóàëüíóþ. Ïîíÿòèå àêòóàëüíîé áåñêîíå&di