Реферат: Цифровые устройства
Максимальное число, которое может быть записано в счетчике, равно числу его состояний и называется модулем счета Ксч . Счетчик , не имеющий дополнительных связей , имеет модуль счета Ксч = 2n . Счетчики, имеющие модуль счета 2n , называются двоичными. Если Ксч ¹ 2n , то счетчик называется не двоичным. Одним из недвоичных является двоично-десятичный счетчик.
1. Суммирующий двоичный асинхронный счетчик с последовательным переносом.
 |
????? ????????? ???????? ? ???????????????? ????????? ?? JK ? ?????????, ??????????? ? ???? 8421, ???????? ?? ??? 1.14.13. ????? JK ? ???????? ?????????? ? ? ? ???????? ????? ?????? ?1? ?? ???? J ? K .
Рис. 1.14.13
Поскольку триггеры имеют инверсный динамический вход, то каждый последующий триггер будет переключаться при сбросе в «0» предыдущего триггера. Важным параметром счетчика является его максимальное время установления кода, т.е. время, необходимое для установления кода после подачи счетного импульса. В схемах счетчиков с последовательным переносом максимальное время установления Туст определяется суммой времени задержки переключения всех триггеров. Время установления Туст определяет быстродействие счетчика. Счетчики с последовательным переносом обладают сравнительно плохим быстродействием.
2. Суммирующий двоичный счетчик с последовательным переносом.
Наличие сигнала переноса в старший разряд определяется выражениями:
P12 = Q1 ×C1 ; P23 = Q1 ×Q2 ×C; P34 = Q1 ×Q2 ×Q3 ×C,
, где Р12 – сигнал переноса из первого разряда во второй; Р23 – сигнал переноса из второго разряда в третий и т.п.
Для любого разряда Pn(n+1) = Q1 ×Q2 ×Q3 , …, Qn ×C . В схеме счетчика с параллельным переносом сигналы переноса в каждый разряд формируются согласно приведенным формулам.
Схема счетчика с параллельным переносом показана на рис 1.1.4.14.
Рис. 1.14.14
Время установления кода при параллельной организации переноса определяется задержкой переключения одного триггера и временем задержки срабатывания схем И и существенно меньше, чем при последовательном переносе.
Недостатком параллельного переноса является то, что при большом числе разрядов требуются схемы И с большим числом входов.
2. Суммирующий счетчик со сквозным переносом.
 |
??? ???????? ???????? ???????? ???????? ???????????? ? ??????, ?????? ?????? ?????? ?????????????? ???????????? ???????, ? ????? ???????? ? ????????????????. ?? ??? 1.14.15 ???????????? ????? ???????? ?? ???????? ?????????, ?????? ?????? ???????? ???????? ?? ??? ????????. ??? ????? ??????????? ???????? ??? ????? ????????? ?????? ???? ?????????????. ????? ???????????? ???? ? ???????? ?? ???????? ????????? ???????????? ????????? ???????????? ????????, ???????? ???????????? ???? ? ? ????????? ? ????? ?????? ? ??????????? ?????. ????? ???????, ?????????????? ?????? ???????? ???????? ????????????? ????? ???????????????? ????????? ? ???????????????? ? ???????????? ?????????.
4. Реверсивный счётчик.
 |
??? ?????????? ??????????? ???????? ?????????? ?????? ?????? ???????? ?? ??????? ???????? ??????? ?? ? ??????? ?????? ??????????? ????????, ? ? ??????????.
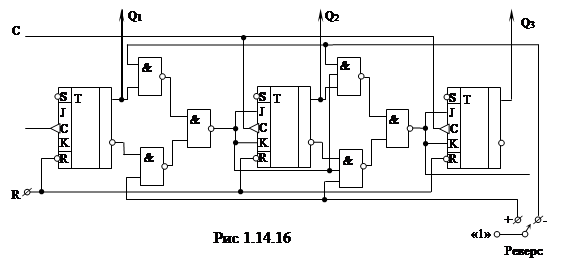Связи между триггерами реверсивного счётчика соответствуют как суммирующему, так и вычитающему счётчику, но работает только одна из связей, которая определяется командой «Реверс» и подается на элемент И–НЕ, включенные в цепи передачи сигнала переноса. Схема реверсивного счётчика показана на Рис 1.14.16.
Пример синтеза двоично-десятичного счетчика.
Пусть требуется синтезировать асинхронный счетчик, работающий в коде 5-2-1-1. В соответствии с заданным кодом заполняем левую часть табл. 1 функционирования счётчика (столбцы Q4 , Q3 , Q2 , Q1 , n).
Таблица 1
| . n | Q4 | Q3 | Q2 | Q1 | J1 | K1 | J2 | K2 | J3 | K3 | J4 | K4 |
| 0 | 0 | 0 | 0 | 0 | 1 | - | 0 | - | - | - | - | - |
| 1 | 0 | 0 | 0 | 1 | - | 0 | 1 | - | - | - | - | - |
| 2 | 0 | 0 | 1 | 1 | - | 0 | - | 1 | 1 | - | - | - |
| 3 | 0 | 1 | 0 | 1 | - | 0 | 1 | - | - | - | - | - |
| 4 | 0 | 1 | 1 | 1 | - | 1 | - | 1 | - | 1 | 1 | - |
| 5 | 1 | 0 | 0 | 0 | 1 | - | 0 | - | - | - | - | - |
| 6 | 1 | 0 | 0 | 1 | - | 0 | 1 | - | - | - | - | - |
| 7 | 1 | 0 | 1 | 1 | - | 0 | - | 1 | 1 | - | - | - |
| 8 | 1 | 1 | 0 | 1 | - | 0 | 0 | - | - | - | - | - |
| 9 | 1 | 1 | 1 | 1 | - | 1 | - | 1 | - | 1 | - | 1 |
В таблице n – номер состояния счетчика, меняющийся на единицу при подаче каждого счетного импульса; Q1 , Q2 , Q3 и Q4 – логические переменные на выходе четырех триггеров, первый триггер с выходом Q1 соответствует первому младшему разряду; J и K – значения соответствующих сигналов на соответствующих входах JK – триггеров.
Каждый из универсальных триггеров может переключаться при подаче на вход С положительного («одиночного») импульса либо при подаче сигнала на вход С с выхода другого триггера. При этом переключение последующего триггера происходит тогда, когда предыдущий переключается из «1» в «0». Учитывая это, находим необходимое место подключения входов С всех четырех триггеров. Первый триггер должен переключаться при подаче первого, пятого и нулевого (десятого) импульса. Ни один из последующих триггеров не может обеспечить всех трех переключений. Поэтому на вход С первого триггер нужно подавать счетные импульсы. Они обеспечивают максимальную частоту переключений, а выборка нужных моментов переключения обеспечивается подачей сигналов на вход J и K .
На вход с второго триггера также нужно подать счетные импульсы, так как выходные сигналы ни одного из триггеров не обеспечат его переключения в нужный момент.
Вход С третьего триггера нужно соединить с выходом второго, так как его переключение при подаче третьего, пятого, восьмого триггера в эти моменты времени из «1» в «0».
По тем же соображениям выход третьего триггера нужно соединить со входом четвертого. Для определения сигналов на входах J и K заполняют правую часть табл. 1, используя таблицу функционирования JK – триггера (табл. 2). Почерк в таблице показывает, что значение сигнала в данном виде не вызывает изменения или сохранения состояния триггера. Например, для переключения первого триггера из «0» в «1» при подаче первого счетного импульса требуется, чтобы J1 = 1 в позиции n = 0,а значения K1 может быть любым, что означает прочерк. Если при очередном такте работы на какой – либо триггер сигнал переноса не подается, т.е. триггер, с которого он может прийти, не сбрасывается в «0», то в соответствующих клетках J и K можно ставить прочерки, так как при любых значениях J и K триггер не переключается. Таким способом заполняется
|
Таблица 2
| Qn ® Qn+1 | Jn | Kn |
| 0 0 | 0 | - |
| 0 1 | 1 | - |
| 1 0 | - | 1 |
| 1 1 | - | 0 |
Перенесем теперь данные правой части табл. 1 на диаграммы Вейча. В табл. 3 приведена диаграмма Вейча для четырех логических переменных. Принимаем за логические переменные значения сигналов на выходах триггеров и заполним восемь диаграмм Вейча (табл. 4), по которым определим сигналы на входах J и K четырех триггеров. При заполнении диаграмм единицы, нули или прочерк ставятся в тех клетках, в которых находятся соответствующие комбинации выходных переменных Q.
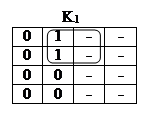Таблица 4
J1
| - | - | - | - |
| - | - | - | - |
| - | - | - | 1 |
| - | - | - | 1 |
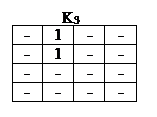
В клетках, в которых функция не определена или её значение не играет роли (т.е. ставится прочерк), можно помещать любые значения переменных, чтобы объединить контуром наибольшее количество клеток. Так, в табл. 4 для J1 во всех клетках можно поставить единицы и объединить одним контуром. Это означает, что J1 = 1.из всех других диаграмм следует, что K1 = Q2 Q3 , J2 =Q1 , K2 = 1, J3 = 1, K3 =1, J4 =1, K4 = 1. Следовательно, на входы J1 , K2 , J3 , K3 , J4 , K4 надо подать единицы, на вход K1 – конъюнкцию сигналов с прямых выходов второго и третьего триггеров, а вход J2 соединить с прямым выходом первого триггера. Если какой либо вход не куда не подключен, это эквивалентно подаче на этот вход единицы. Таким образом, счетчик синтезирован. Его схема показана на рис. 1.14.17.
 |
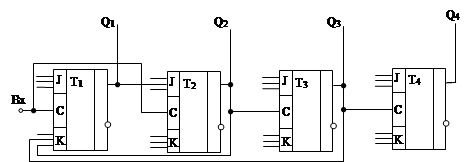Рис 1.14.17
Синтез синхронных счетчиков производится аналогично, но счетные импульсы подаются на входы С всех триггеров, поэтому при подаче каждого счетного импульса в каждом триггере нужно обеспечивать нужные значения J и K.